Método de estratificación
Identificación de datos atípicos
Para hacer cumplir la definición de los límites en el método de estratificación [véase: Método de estratificación de Dalenius & Hodges] y el número óptimo de clases basados en la media aritmética, es importante la identificación de datos atípicos porque podrían ocasionar resultados poco adecuados. Para contrarrestar este problema, Hubert y Vandervieren (2007) proponen el método de caja, el cual toma en cuenta el grado de asimetría de un conjunto de datos.
\[\left[Q_{1} - 1.5e^{-4MC} IQR; \hspace{0.5cm} Q_{3} + 1.5e^{-4MC} IQR \right] \text{para } MC \geq 0\]
\[\left[Q_{1} - 1.5e^{-3MC} IQR; \hspace{0.5cm} Q_{3} + 1.5e^{-3MC} IQR \right] \text{para } MC < 0\]
donde:
\(\circ \:𝑄_{1}\) 𝑦 \(𝑄_{3}\): hacen referencia al primer y tercer cuartil, respectivamente; la diferencia entre estos dos valores da como resultado el valor de espacio intercuartil (\(𝐼𝑄𝑅\)), y
\(\circ \:𝑀𝐶 (𝑚𝑒𝑑𝑐𝑜𝑢𝑝𝑙𝑒)\): cuantifica el grado de asimetría de una muestra univariable \({𝑥_1,𝑥_2,… ,𝑥_𝑛}\).
Se identifican los valores atípicos para cada conjunto de datos.
- Se calculan los estadísticos de la columna del índice de marginación para cada conjunto de datos \(DP2_{i}\) correspondientes al año y se asigna el resultado a una nueva variable denominada \(outliers_i\).
assign(paste0("outliers_2020"), boxplot.stats(DP2_2020[,24]))Se crea un data.frame que contiene el número de valores atípicos, su rango y el límite inferior para cada conjunto de datos.
| Límites para el cálculo de estratificación a nivel colonia, 2020 | ||
| Mínimo | Límite | |
|---|---|---|
Se identifican los casos extremos en el índice de marginación y se aplica el método de caja propuesto por Hubert y Vandervieren, concluyendo los límites con los que se debe trabajar.
Se añade una nueva columna IM_out. Esta columna se calcula usando if_else, de la siguiente manera:
- Si el valor de IM es mayor o igual al límite inferior de los valores no considerados outliers
(get(paste0("outliers_", i))$stats[1]), entoncesIM_outtoma el valor deIM.
- Si el valor de IM es menor que el límite inferior, entonces
IM_outtoma el valor del límite inferior, eliminando así los outliers.
Método de estratificación de Dalenius & Hodges
strata.cumrootf: cumulative root frequency method by Dalenius and Hodges (1959).
Con la obtención del índice de marginación a través del método DP2, los valores se clasificaron en cinco categorías ordinales con el método de Dalenius y Hodges (1959), para obtener el grado de marginación. Este método forma estratos de manera que la varianza sea mínima al interior de cada estrato y máxima entre cada uno de ellos, es decir, son lo más homogéneos posibles. Este procedimiento utiliza la raíz de las frecuencias acumuladas para la construcción de los estratos, por lo que se lleva a cabo para la división de la población en el estrato L. Esta es una solución aproximada de Dalenius y Hodges (1959) a las ecuaciones de Dalenius (1950). De acuerdo con Gunning y Horgan (2004), el límite superior de cada estrato se determinó con la siguiente expresión:
\[Q = \frac{1}{L}\sum^{J}_{i=1}{\sqrt{f_{i}}}\]
Sea un conjunto de estratos determinados por su límite superior,
\[Q,\ 2Q,\ \ldots,\ \left(L-1\right)Q,\ (L)Q.\] donde:
\(\circ \:J\): es el número de clases dentro del grupo de la variable ordenada X,
\(\circ \:f_{i}\ \in(1,\ \ldots, J)\): es la frecuencia en cada clase \(J\), y
\(\circ \:L\): es el número de estratos.
La eficiencia del método de la raíz de las frecuencias acumuladas depende principalmente del número de clases dentro del grupo de la variable ordenada. Sin embargo, no hay un procedimiento estándar sobre cómo elegir el mejor valor para el número de clases, siendo esto una limitante del método de Dalenius y Hodges. Para medir el efecto del número de clases en la varianza de cada estrato se recurrió a un método iterativo para obtener un criterio de agrupación óptimo.
Para establecer los límites de los estratos \((b_{1},\ \ldots,\ b_{L})\) que minimicen la varianza del estimador, se utiliza la asignación de Neyman para determinar el tamaño de muestra óptimo. Sea la varianza del estimador:
\[V\left({\bar{x}}_{st}\right)=\ \sum_{h}\left(\frac{N_h}{N}\right)^2\frac{S_h^2}{n_h}\ \] donde:
\(\circ \: S_{h}^{2}\): es la varianza poblacional en el estrato \(h\),
\(\circ \:n_{h}\): es el tamaño de muestra en el estrato \(h\) utilizada por la asignación de Neyman, y
\(\circ \:N_{h}\): es el total de elementos en el estrato \(h\), sea \(N=\sum_{h=1}^{L}{N_{h}}\).
Si se asume que la distribución dentro de cada estrato se distribuye aproximadamente de manera uniforme, los límites se obtienen tomando intervalos iguales en la función de la raíz de las frecuencias acumuladas. Los límites se resuelven de manera iterativa:
\[\frac{S_h^2+(b_h-{\bar{X}}_h)2}{S_h}=\frac{S_{h+1}^2+(b_h-{\bar{X}}_{h+1})2}{S_{h+1}}\ para\ h=1,\ \ldots.\ ,\ L-1\] donde:
\(\circ \: b_{h}\): es el límite superior en el estrato \(h\),
\(\circ \: {\bar{X}}_{h}\): es la media poblacional en el estrato \(h\), y
\(\circ \: S_{h}^{2}\): es la varianza poblacional en el estrato \(h\).
El requisito de precisión, generalmente se establece cuando el coeficiente de variación sea igual a un nivel especificado entre 1 y 10 por ciento (Hidiroglou y Kozak, 2018).
Número óptimo de clases del método de Dalenius & Hodge
alloc lista que especifica el esquema de asignación. La lista debe contener 3 números para los 3 exponentes q1, q2 y q3 en el esquema de asignación general (ver paquete de stratification). El valor predeterminado es la asignación de Neyman (q1 = q3 = 0.5 y q2 = 0)
A continuación, se realiza un análisis de estratificación sobre los diferentes años, usando la función strata.cumrootf(), almacenando los resultados de errores estándar, medias y varianzas en matrices que luego se guardan en listas.
iteraciones <- 1000
start.time <- Sys.time()
i <- 1
sd <- matrix(NA, nrow = (iteraciones), ncol = 3)
meanh <- matrix(NA, nrow = (iteraciones), ncol = 6)
varh <- matrix(NA, nrow = (iteraciones), ncol = 6)
for (n in seq(5, iteraciones, 1)){
cum <- strata.cumrootf(x = DP2_2020[,25], CV = 0.05 , Ls = 5, alloc = c(0.5, 0, 0.5), nclass = n)
sd[i,] <- c(n, cum$stderr, cum$CV)
meanh[i,] <- c(n, cum$meanh)
varh[i,] <- c(n, cum$varh)
i <- i + 1
}
colnames(sd) <- c("n", "sderr", "CV")
colnames(meanh) <- c("nclass", paste0(rep("Strata", 5), 1:5))
colnames(varh) <- c("nclass", paste0(rep("Strata", 5), 1:5))
end.time <- Sys.time()
time.taken <- round(end.time - start.time, 2)
time.takenNúmero óptimo de clases
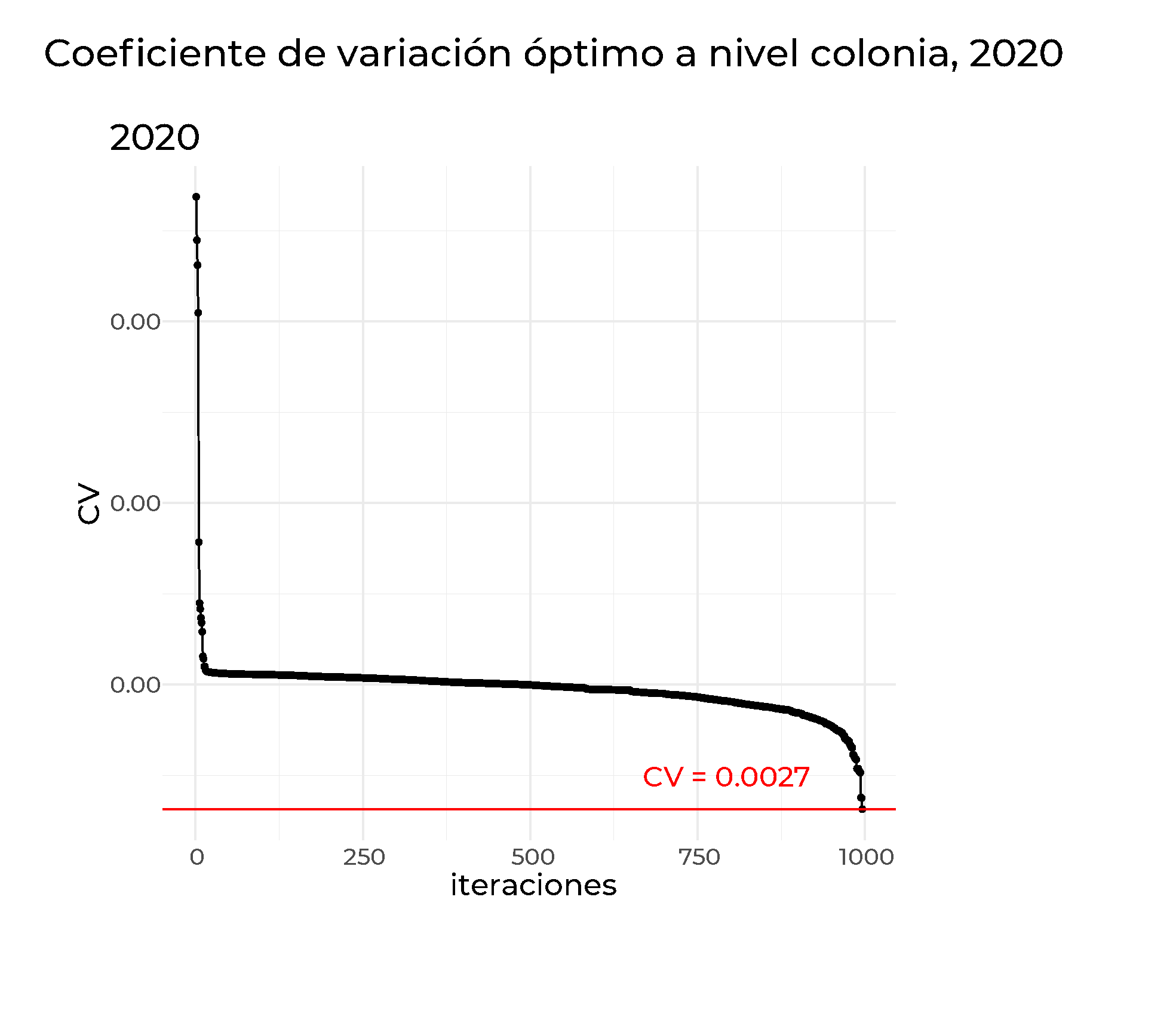
Se toma cada matriz resultante de errores estándar de la lista stderr, y luego selecciona la fila que tiene el coeficiente de variación (CV) más bajo. Estos resultados se almacenan en la lista min.strata, la cual contendrá los data.frames correspondientes a las filas con el menor CVpara cada uno de los tres conjuntos de datos en stderr.
min.strata <- sd %>%
as.data.frame() %>%
slice(which.min(.$CV)) | Número óptimo de clases | |||
| AÑO | n | sd | C.V. |
|---|---|---|---|
Se toman en cuenta el número de clases que salen del los resultados del método iterativo. Utilizando la función strata.cumrootf() de la paquetería stratification con parámetros específicos y el número de clases (nclass) obtenido de min.strata.
- CV = 0.05: Establece el coeficiente de variación.
- Ls = 5: Establece el número de estratos.
- alloc = c(0.5, 0, 0.5): Define la asignación para la estratificación.
- nclass = min.strata[,1]: Establece el número de clases utilizando el primer valor de la fila con el menor CV en min.strata.
strata.DP2 <- strata.cumrootf(DP2_2020[,25],
CV = 0.01,
Ls = 5,
alloc = c(0.5, 0, 0.5),
nclass = min.strata[,1])Se agregan los datos a la base original
##Se agrega a la base DP2
DP2_2020 <- data.frame(DP2_2020 %>%
select(-IM_out), ## Se elimina el índice ficticio
strata.DP2[["stratumID"]])
# Se cambian los nombres de las columnas
names(DP2_2020) <- c(names(DP2_2020)[1:23],
paste0("IM_2020"), paste0("GM_2020"))
# Se cambian los levels a los grados de marginación correspondientes
levels(DP2_2020[,25]) = c("Muy alto", "Alto", "Medio", "Bajo", "Muy bajo")Límites de los estratos
Se crea un data frame llamado limites que contiene los límites de ciertos intervalos para el año 2020. Cada columna contiene una combinación de:
- El valor mínimo del índice de marginación (IM:) para el año correspondiente.
- Los valores de los límites de los estratos (bh) calculados previamente.
- El valor máximo del índice de marginación (IM_) para el año correspondiente.
limites <- data.frame("2020" = c(min(DP2_2020$IM_2020), strata.DP2$bh, max(DP2_2020$IM_2020)))| Límite de los estratos | |||||
| Muy alto | Alto | Medio | Bajo | Muy bajo | |
|---|---|---|---|---|---|
| 2020 | |||||