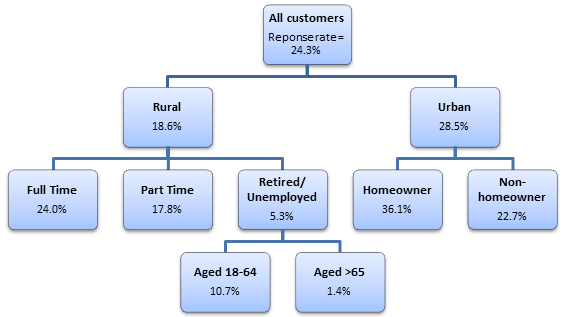
🌲 2. Árboles de Decisión y Derivados
Ejemplos: Árbol de Decisión, Random Forest, Gradient Boosting.
Uso: Excelentes para datos tabulares con relaciones no lineales, incluyendo variables categóricas y numéricas. Son una buena opción cuando la interpretabilidad es clave.
Ventajas: Pueden manejar diversos tipos de datos y, los árboles individuales, son fáciles de interpretar.
Limitaciones: Los árboles simples pueden sobreajustarse, y su rendimiento baja con datos muy ruidosos si no se usan métodos de ensamble.
C4.5
C4.5 es una extensión del algoritmo ID3, también desarrollado por Ross Quinlan, y es uno de los algoritmos de árboles de decisión más influyentes y ampliamente utilizados para tareas de clasificación. Fue diseñado para abordar algunas de las limitaciones de su predecesor, ID3, y se ha convertido en un estándar de facto en el aprendizaje automático para construir modelos predictivos interpretables.
Al igual que ID3, C4.5 construye un árbol de clasificación seleccionando en cada nodo el atributo que mejor divide el conjunto de datos. Sin embargo, en lugar de usar solo la ganancia de información, C4.5 utiliza la relación de ganancia (Gain Ratio). La relación de ganancia normaliza la ganancia de información por la entropía intrínseca del atributo, lo que ayuda a mitigar el sesgo de ID3 hacia atributos con muchos valores. Además, C4.5 introduce varias mejoras significativas:
- Manejo de atributos continuos: Puede discretizar atributos numéricos continuos dividiendo el rango en intervalos.
- Manejo de valores faltantes: Puede manejar datos con valores ausentes asignando una probabilidad fraccionada a cada rama posible.
- Poda del árbol: Implementa una técnica de poda para reducir el sobreajuste, lo que implica eliminar ramas del árbol que no aportan significativamente a la clasificación o que representan ruido en los datos.
En el contexto del aprendizaje global vs. local, C4.5, al igual que ID3 y CART, opera como un sistema de aprendizaje local. La construcción del árbol se logra a través de decisiones de división que se optimizan localmente en cada nodo, buscando la máxima homogeneidad o pureza en los subconjuntos resultantes. Esto le permite a C4.5 manejar eficazmente relaciones no lineales entre las variables independientes y dependientes. La idea es que, si los datos no se distribuyen linealmente, el concepto de regresión (o clasificación) se puede aplicar de forma efectiva mediante esta regresión ponderada localmente, donde el algoritmo divide el problema de aprendizaje global en múltiples problemas de aprendizaje más pequeños y simples. Al centrarse en divisiones óptimas a nivel de subconjuntos, C4.5 ofrece una alternativa robusta a los métodos de aproximación de funciones globales, que a veces pueden fallar en proporcionar una buena aproximación cuando la relación entre las variables no es lineal.
| Guía rápida para elegir C4.5 | ||
| Criterio | Aplica | Detalles |
|---|---|---|
| Fuente: Elaboración propia | ||
C5.0
C5.0 es la versión más reciente y avanzada de los algoritmos de árboles de decisión desarrollados por Ross Quinlan, sucediendo a ID3 y C4.5. Es un algoritmo propietario (aunque se ofrece una versión de código abierto bajo ciertas licencias) y es ampliamente reconocido por su rapidez, precisión y eficiencia en la construcción de árboles de decisión y reglas de clasificación para tareas de clasificación.
Al igual que sus predecesores, C5.0 construye un árbol de clasificación mediante la división recursiva de los datos en subconjuntos más homogéneos. Sin embargo, C5.0 incorpora mejoras significativas que lo hacen superior en muchos aspectos:
- Velocidad y eficiencia: Es notablemente más rápido y más eficiente en el uso de memoria que C4.5, lo que le permite manejar conjuntos de datos mucho más grandes.
- Impulso (Boosting): C5.0 puede usar la técnica de boosting (específicamente, una variante de AdaBoost) para crear múltiples árboles de decisión y combinarlos para producir una predicción más robusta y precisa. Esto reduce significativamente los errores de clasificación y mejora la generalización.
- Poda mejorada: Ofrece técnicas de poda más sofisticadas para evitar el sobreajuste y producir árboles más pequeños y comprensibles.
- Manejo de valores faltantes y atributos continuos: Al igual que C4.5, maneja de manera efectiva valores faltantes y atributos numéricos continuos.
- Generación de reglas: Además de árboles de decisión, C5.0 puede generar conjuntos de reglas de clasificación concisas, que a menudo son más fáciles de interpretar que un árbol completo.
En el contexto de la regresión localmente ponderada, C5.0, como los demás algoritmos de árboles de decisión, opera bajo la premisa de un aprendizaje local. La construcción del árbol implica tomar decisiones de división óptimas en cada nodo, basándose en la información local de ese subconjunto de datos. Si los datos no se distribuyen linealmente, el concepto de regresión (o clasificación, que es su enfoque principal) se puede aplicar eficazmente al dividir el problema de aprendizaje global en múltiples problemas de aprendizaje más pequeños y simples. Cada división en el árbol se puede ver como una forma de regresión ponderada localmente, donde el algoritmo se enfoca en aproximar la relación dentro de un subespacio específico del conjunto de datos. Esto convierte a C5.0 en una potente alternativa a los métodos de aproximación de funciones globales, especialmente cuando la relación entre las variables independientes y dependientes no es lineal y se busca un modelo interpretable y robusto.
| Guía rápida para elegir C5.0 | ||
| Criterio | Aplica | Detalles |
|---|---|---|
| Fuente: Elaboración propia | ||
Classification and Regression Tree (CART)
Classification and Regression Tree (CART) es un método no paramétrico que se utiliza para construir árboles de decisión tanto para problemas de clasificación como de regresión. La idea central es dividir recursivamente el espacio de las características en regiones más pequeñas y manejables, creando así un modelo con forma de árbol que es fácil de interpretar.
A diferencia de los modelos lineales o algunos algoritmos de aprendizaje global, CART no asume una relación lineal entre las variables. En su lugar, el algoritmo identifica los mejores puntos de división en las variables predictoras para maximizar la homogeneidad de las respuestas dentro de cada región resultante. Para problemas de clasificación, esto se mide comúnmente con métricas como la impureza Gini o la ganancia de información, mientras que para la regresión, se busca minimizar la suma de los cuadrados de los residuos.
Mientras que muchos algoritmos (como las redes neuronales clásicas o las máquinas de vectores de soporte) son sistemas de aprendizaje global que buscan minimizar una función de pérdida única para todo el conjunto de datos, CART se puede considerar más como un sistema de aprendizaje local. Construye el modelo tomando decisiones de división locales en cada nodo del árbol, lo que le permite capturar relaciones complejas y no lineales en los datos. Esto es particularmente útil cuando una aproximación de función global única podría no ser suficiente para modelar la relación entre las variables. Una de las ventajas de CART es su capacidad para manejar diferentes tipos de datos (numéricos y categóricos) y su interpretabilidad, ya que la ruta desde la raíz hasta una hoja del árbol representa un conjunto de reglas de decisión.
| Guía rápida para elegir CART | ||
| Classification and Regression Tree (CART) | ||
| Criterio | Aplica | Detalles |
|---|---|---|
| Fuente: Elaboración propia | ||
Chi-squared Automatic Interaction Detection (CHAID)
Chi-squared Automatic Interaction Detection (CHAID) es un algoritmo de árboles de decisión utilizado principalmente para tareas de clasificación y, en menor medida, para la regresión (aunque se aplica más comúnmente a variables dependientes categóricas). La idea fundamental de CHAID es construir un árbol de decisión al encontrar las mejores divisiones en las variables predictoras que maximicen la significancia estadística de la relación con la variable dependiente.
A diferencia de ID3, C4.5 o CART, que utilizan medidas de impureza como la entropía o el índice Gini, CHAID se basa en pruebas estadísticas de chi-cuadrado (\(\chi^2\)) para identificar las divisiones óptimas. Cuando la variable dependiente es nominal o ordinal, CHAID evalúa cada variable predictora para encontrar la combinación de categorías que sea más significativamente diferente de otras combinaciones en términos de la distribución de la variable dependiente. El algoritmo fusiona las categorías de una variable predictora si no son significativamente diferentes, y luego selecciona la variable predictora y la división que resultan en el valor más bajo de \(p\) (es decir, la mayor significancia estadística) de la prueba \(\chi^2\). Para variables dependientes continuas, se utiliza una prueba F.
En el contexto del aprendizaje global vs. local, CHAID opera como un sistema de aprendizaje local. La construcción del árbol es un proceso iterativo y recursivo donde las decisiones de división se toman en cada nodo basándose en la significancia estadística local de la interacción entre las variables predictoras y la variable dependiente. Esto le permite a CHAID descubrir relaciones complejas y no lineales en los datos. La idea es que, si los datos no se distribuyen linealmente, se puede aplicar el concepto de regresión (o clasificación) de manera efectiva mediante lo que se denomina regresión ponderada localmente. Esto se logra al dividir el problema de aprendizaje global en múltiples problemas de aprendizaje más pequeños y simples, donde cada rama del árbol representa una región del espacio de características donde las interacciones son evaluadas y modeladas localmente. Esto hace de CHAID una alternativa robusta a los métodos de aproximación de funciones globales, especialmente cuando se busca un modelo interpretable y se quieren identificar las interacciones entre las variables de una manera estadísticamente rigurosa.
| Guía rápida para elegir CHAID | ||
| Chi-squared Automatic Interaction Detection (CHAID) | ||
| Criterio | Aplica | Detalles |
|---|---|---|
| Fuente: Elaboración propia | ||
Conditional Decision Trees (Conditional Inference Trees - CITs)
Conditional Decision Trees, often referred to as Conditional Inference Trees (CITs), represent a class of árboles de decisión que abordan una limitación importante de los algoritmos de árboles de decisión tradicionales como CART, ID3, y C4.5: el sesgo en la selección de variables. Mientras que los algoritmos tradicionales pueden favorecer variables predictoras con muchas categorías o valores continuos (debido a que estas variables tienen más “oportunidades” de generar una división que parezca óptima), los CITs emplean un enfoque basado en pruebas estadísticas para seleccionar la mejor división.
La idea fundamental de los Conditional Decision Trees es que cada división en el árbol se basa en la significancia estadística de la asociación entre las variables predictoras y la variable de respuesta. En lugar de seleccionar el atributo que maximiza una medida de impureza (como la ganancia de información o la impureza Gini), los CITs realizan una serie de pruebas de inferencia condicional (típicamente pruebas de permutación).
El algoritmo opera de la siguiente manera: 1. En cada nodo, se evalúa una hipótesis nula de independencia entre cada variable predictora y la variable de respuesta. 2. Se calcula el valor de \(p\) para cada variable predictora. 3. La variable predictora con el valor de \(p\) más pequeño (es decir, la asociación más estadísticamente significativa) es seleccionada para la división, siempre y cuando este valor de \(p\) sea menor que un umbral de significancia predefinido. 4. Una vez seleccionada la variable, se encuentra la mejor división binaria (generalmente) dentro de esa variable para ese nodo. 5. Este proceso se repite recursivamente hasta que no haya más variables significativas para dividir o se alcance un criterio de parada.
En el contexto del aprendizaje global vs. local, los Conditional Decision Trees se pueden considerar como un enfoque de aprendizaje local con un fuerte respaldo estadístico. Aunque el árbol resultante es un modelo global, cada decisión de división se toma localmente basándose en la inferencia estadística sobre la relación entre las variables en ese subconjunto de datos. Esto significa que si los datos no se distribuyen linealmente, el concepto de regresión (o clasificación) se aplica de forma efectiva mediante lo que se denomina regresión ponderada localmente. Al utilizar pruebas de significancia para las divisiones, los CITs evitan el problema de que “a veces ningún valor de parámetro puede proporcionar una aproximación suficientemente buena” en una única aproximación global, ya que las divisiones se determinan por la evidencia estadística local. Esto los convierte en una alternativa robusta que ofrece una selección de variables menos sesgada y modelos con una mayor interpretabilidad estadística.
| Guía rápida para elegir ctree | ||
| Conditional Decision Trees | ||
| Criterio | Aplica | Detalles |
|---|---|---|
| Fuente: Elaboración propia | ||
Cubist
Cubist es un algoritmo de Machine Learning desarrollado por RuleQuest Research (autores de C4.5 y See5/C5.0), principalmente para tareas de regresión. Es una extensión de los modelos de árboles de decisión que combina la simplicidad de las reglas con la precisión de los modelos locales, lo que lo hace muy potente para datos complejos con muchas características.
En esencia, Cubist construye un modelo de reglas con un modelo lineal adjunto a cada regla. Opera en dos fases principales:
-
Construcción del Árbol de Reglas:
- Similar a un árbol de decisión, Cubist construye una estructura de árbol dividiendo los datos en subconjuntos basados en los valores de las características.
- Sin embargo, en lugar de hojas que contienen un valor constante (como en los árboles de regresión tradicionales), cada hoja de este árbol se transforma en un conjunto de reglas.
- A cada regla se le asocia un modelo lineal multivariado local (o un “modelo de comité” de reglas, donde varias reglas contribuyen a la predicción). Este modelo lineal se entrena solo con los datos que satisfacen las condiciones de esa regla.
-
Ajuste del Modelo de Reglas y Predicción:
- Para cada nueva instancia de predicción, Cubist identifica las reglas que se aplican a esa instancia.
- La predicción final se calcula combinando las predicciones de los modelos lineales de las reglas que se aplican, y luego se ajusta un poco esa predicción mediante un “comité” de vecinos (ajustes locales adicionales basados en ejemplos similares), si está configurado para ello. Esta etapa de ajuste lo hace aún más robusto.
Cubist es valorado por su capacidad para manejar relaciones complejas y no lineales en los datos. Proporciona un modelo que es más interpretable que una “caja negra” (como una red neuronal profunda) debido a su base en reglas, pero mucho más preciso que los modelos lineales o los árboles de regresión simples, gracias a sus modelos lineales locales y ajustes.
Aprendizaje Global vs. Local:
Cubist es un algoritmo que combina de manera muy efectiva aspectos de aprendizaje global y local.
Aspecto Global (Estructura de Reglas): La fase de construcción del árbol y la derivación de las reglas crean una estructura global que divide el espacio de características. Este conjunto de reglas abarca todo el dominio de los datos y determina qué modelo local se aplicará a una instancia. Es una forma de particionar el espacio de características de manera jerárquica para establecer un marco de predicción general.
-
Aspecto Local (Modelos Lineales y Ajustes): Aquí es donde Cubist brilla en su capacidad de aprendizaje local:
- Modelos Lineales Locales: Cada regla tiene asociado un modelo lineal que se entrena solo con los datos que caen dentro de esa regla. Esto permite a Cubist capturar relaciones locales y no lineales de manera precisa. En lugar de una única relación lineal global, el modelo se adapta a las particularidades de diferentes subregiones de los datos.
-
Ajuste Basado en Vecinos: Si se activa la opción de “comité” o el ajuste basado en vecinos (conocido como
committeesoneighbors), el modelo refina aún más su predicción incorporando la información de los ejemplos de entrenamiento más cercanos al punto de consulta. Esto es una forma de “regresión ponderada localmente”, donde la predicción final se ajusta en función de los patrones observados en el vecindario inmediato del punto de interés.
| Guía rápida para elegir cubist | ||
| Cubist | ||
| Criterio | Aplica | Detalles |
|---|---|---|
| Fuente: Elaboración propia | ||
Decision Stump
Un Decision Stump es el tipo de árbol de decisión más simple y fundamental, compuesto por un único nodo de decisión (la raíz) que se conecta directamente a los nodos hoja. La idea es que un decision stump toma una decisión de clasificación o regresión basándose en una sola característica o atributo de entrada.
Aunque parece demasiado simple, la lógica es que, a pesar de su simplicidad, un decision stump identifica el mejor umbral o categoría dentro de una única variable para separar los datos de la manera más efectiva posible. Para problemas de clasificación, esto significa encontrar la característica que, por sí sola, maximice alguna medida de pureza (como la ganancia de información, la impureza Gini, o la significancia chi-cuadrado) o minimice el error de clasificación. Para regresión, buscará el punto de división en una sola característica que minimice la suma de los cuadrados de los errores.
En el contexto del aprendizaje local vs. global, un decision stump es inherentemente un sistema de aprendizaje local. Su “aprendizaje” se limita a encontrar la mejor división dentro de una única variable, lo que es una forma extrema de regresión ponderada localmente. Si los datos no se distribuyen linealmente, un decision stump no puede por sí mismo modelar relaciones complejas. Sin embargo, su valor no reside en ser un modelo predictivo robusto por sí mismo, sino en ser un “clasificador débil” o “regresor débil” que puede ser combinado en conjuntos de modelos (ensembles) más potentes. Por ejemplo, los decision stumps son los bloques de construcción más comunes para algoritmos de boosting como AdaBoost. En estos casos, múltiples decision stumps se entrenan secuencialmente, cada uno enfocándose en los errores que cometieron los stumps anteriores, sumando sus “aprendizajes locales” para formar un modelo global más preciso. Esto contrarresta la limitación de que “a veces ningún valor de parámetro puede proporcionar una aproximación suficientemente buena” en un solo modelo.
| Guía rápida para elegir Decision Stump | ||
| Decision Stump | ||
| Criterio | Aplica | Detalles |
|---|---|---|
| Fuente: Elaboración propia | ||
Iterative Dichotomiser 3 (ID3)
Iterative Dichotomiser 3 (ID3) es un algoritmo clásico para construir árboles de decisión, diseñado principalmente para tareas de clasificación. Fue uno de los primeros algoritmos de árboles de decisión desarrollados por Ross Quinlan. La idea central de ID3 es construir un árbol de clasificación seleccionando en cada nodo del árbol el atributo que mejor divide el conjunto de datos en subconjuntos más puros y homogéneos.
ID3 opera de forma iterativa y dicotómica (aunque puede manejar atributos con más de dos categorías), dividiendo el conjunto de datos en cada paso basándose en el atributo más informativo. La selección del “mejor” atributo se basa en métricas de teoría de la información, principalmente la ganancia de información (Information Gain). La ganancia de información mide la reducción en la entropía (una medida de la impureza o desorden de un conjunto de datos) que se logra al dividir los datos según un atributo particular. El atributo con la mayor ganancia de información es elegido como el nodo de decisión en cada nivel del árbol.
A diferencia de los sistemas de aprendizaje global que buscan minimizar funciones de pérdida globales (como el error cuadrático medio), ID3 es un algoritmo de aprendizaje local en el sentido de que toma decisiones de división óptimas en cada nodo basándose en la información disponible en ese subconjunto de datos. Aunque la construcción del árbol es un proceso global, cada paso de la división se optimiza localmente para maximizar la pureza de los subconjuntos resultantes. Esto le permite a ID3 capturar relaciones no lineales entre las variables, ya que no asume una distribución lineal de los datos. En esencia, si los datos no se distribuyen linealmente, se puede aplicar el concepto de regresión (o clasificación, en este caso) de manera ponderada localmente al dividir el espacio de características en regiones más manejables. Sin embargo, una desventaja de ID3 es que tiende a favorecer atributos con muchos valores y puede ser propenso al sobreajuste.
| Guía rápida para elegir IDE3 | ||
| Iterative Dichotomiser 3 (ID3) | ||
| Criterio | Aplica | Detalles |
|---|---|---|
| Fuente: Elaboración propia | ||
M5 (Model Tree)
.png)
M5, a menudo referida como M5’ o M5P (su implementación en el software Weka), es un algoritmo de árboles de decisión específicamente diseñado para tareas de regresión, es decir, para predecir valores numéricos continuos. Desarrollado por Ross Quinlan en 1992 y luego mejorado por Wang y Witten en 1997, M5 se destaca de los árboles de regresión tradicionales (como los de CART que solo tienen valores constantes en las hojas) al incorporar modelos de regresión lineal en sus nodos hoja.
La idea fundamental de M5 es combinar la interpretabilidad de un árbol de decisión con la capacidad predictiva de los modelos de regresión lineal. Funciona en dos etapas principales:
Construcción del Árbol: M5 construye un árbol de decisión de forma recursiva, similar a otros algoritmos de árboles. Sin embargo, en lugar de usar medidas de impureza para clasificación, utiliza la reducción de la desviación estándar (SDR) como criterio de división. El algoritmo selecciona el atributo y el punto de división que maximizan la reducción de la desviación estándar del valor objetivo en los subconjuntos resultantes. Este proceso continúa hasta que el número de instancias en un nodo es muy pequeño o la desviación estándar es muy baja.
Poda y Suavizado: Una vez construido el árbol inicial, M5 lo poda para evitar el sobreajuste. En lugar de reemplazar los nodos con un valor constante, los nodos hoja (y a veces nodos internos) son reemplazados por modelos de regresión lineal multivariados. Estos modelos lineales se construyen utilizando los atributos relevantes para esa rama del árbol. Además, M5 aplica un proceso de suavizado para compensar las discontinuidades bruscas que podrían surgir entre las predicciones de modelos lineales adyacentes. Este suavizado ajusta el valor predicho en una hoja basándose en las predicciones de los modelos en los nodos a lo largo de la ruta desde la raíz hasta esa hoja.
En el contexto del aprendizaje global vs. local, M5 es un híbrido interesante. Por un lado, la construcción del árbol se basa en decisiones de división locales, buscando la mejor reducción de la desviación estándar en cada nodo. Esto permite a M5 modelar relaciones no lineales, ya que “si los datos no se distribuyen linealmente, se puede aplicar el concepto de regresión de manera ponderada localmente”. El árbol divide el problema de regresión global en múltiples subproblemas más pequeños. Por otro lado, al tener modelos de regresión lineal en las hojas, M5 incorpora un componente de aproximación de función local más sofisticado que un simple valor constante. Estos modelos lineales son “locales” para la región de datos que representa esa hoja, pero internamente son modelos globales para esa subregión. Esto permite a M5 ofrecer una alternativa potente a las aproximaciones de funciones puramente globales, especialmente cuando las relaciones entre las variables son complejas y se benefician de una combinación de particionamiento del espacio y modelado lineal dentro de esas particiones.
| Guía rápida para elegir M5 | ||
| M5 model tree algorithm | ||
| Criterio | Aplica | Detalles |
|---|---|---|
| Fuente: Elaboración propia | ||