📏 9. Clustering (Aprendizaje No Supervisado)
Ejemplos: K-Means, DBSCAN, Agrupamiento Jerárquico.
Uso: Excelente para agrupar datos sin etiquetas previas, permitiéndote descubrir estructuras ocultas o identificar segmentos de mercado dentro de tus conjuntos de datos. Es una herramienta clave en la exploración de datos.
Ventajas: Es increíblemente útil para la exploración de datos y para reducir la complejidad al encontrar patrones inherentes.
Limitaciones: Generalmente, necesitas elegir el número de grupos de antemano (excepto en DBSCAN), lo cual puede ser un desafío. Además, algunos algoritmos pueden ser sensibles a la escala de las características de tus datos.
Density-Based Spatial Clustering of Applications with Noise (DBSCAN)
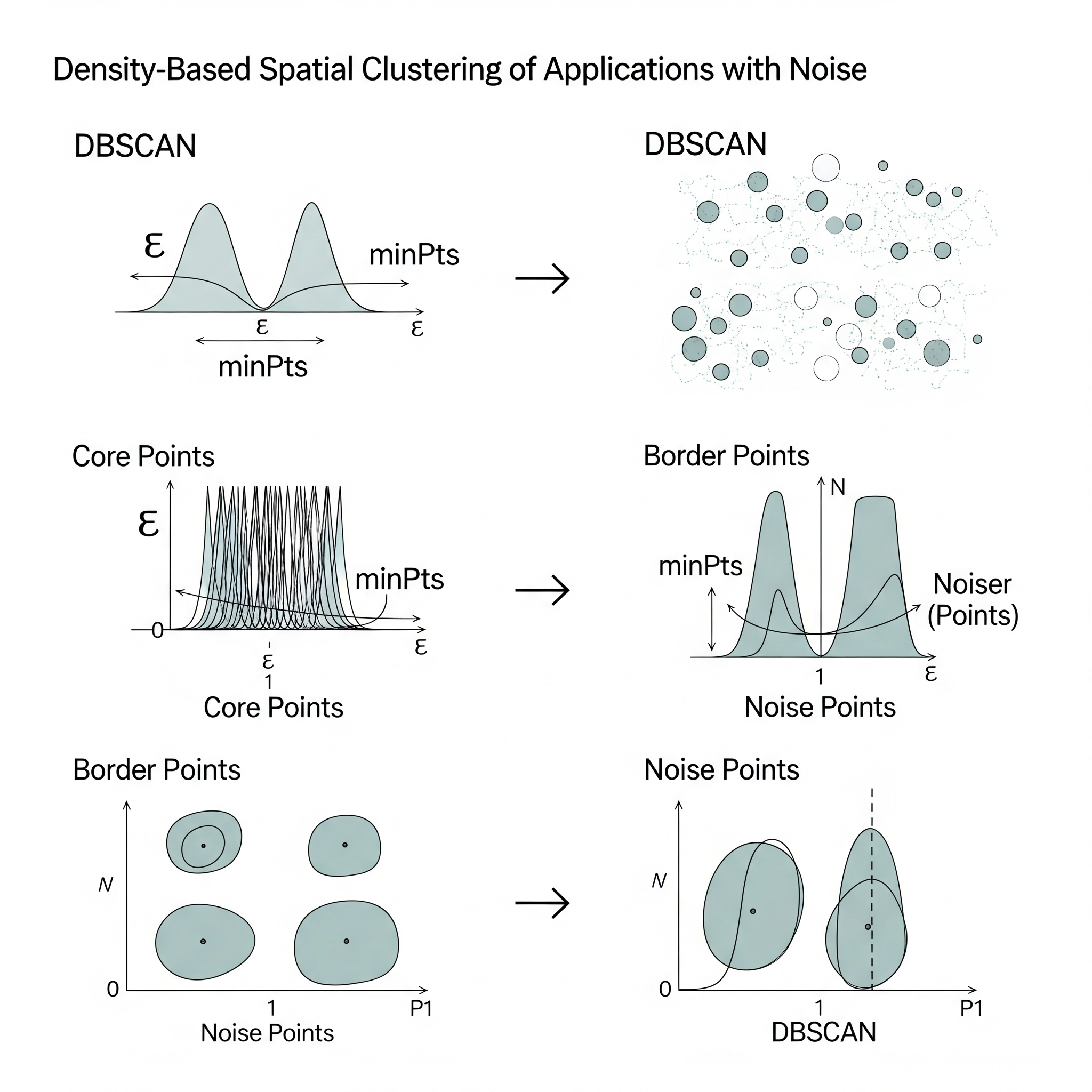
DBSCAN (Density-Based Spatial Clustering of Applications with Noise) es un algoritmo de agrupamiento (clustering) no supervisado que se distingue de los algoritmos basados en centroides (como k-Means) por su capacidad para encontrar clusters de formas arbitrarias y para identificar puntos de ruido (outliers). Su idea central es que los clusters son regiones densas de puntos en el espacio de características, separadas por regiones de baja densidad.
DBSCAN define tres tipos de puntos:
-
Punto Núcleo (Core Point): Un punto es un punto núcleo si, dentro de un radio especificado (\(\epsilon\) o
eps), contiene un número mínimo de otros puntos (MinPts). -
Punto Frontera (Border Point): Un punto es un punto frontera si está dentro del radio \(\epsilon\) de un punto núcleo, pero no es un punto núcleo en sí mismo (no tiene
MinPtsvecinos dentro de su propio radio \(\epsilon\)). - Punto de Ruido (Noise Point): Cualquier punto que no es un punto núcleo ni un punto frontera. Estos puntos son considerados outliers.
El algoritmo de DBSCAN opera de la siguiente manera:
- Inicialización: Selecciona un punto arbitrario del conjunto de datos que aún no ha sido visitado.
-
Expansión de Cluster:
- Si el punto seleccionado es un punto núcleo, se inicia un nuevo cluster. Todos sus vecinos dentro del radio \(\epsilon\) se añaden al cluster.
- Recursivamente, se visitan y añaden los vecinos de esos nuevos puntos. Si un vecino es también un punto núcleo, sus propios vecinos también se añaden al cluster. Este proceso continúa hasta que no se puedan añadir más puntos al cluster (es decir, todos los puntos alcanzables por densidad han sido encontrados).
- Si el punto seleccionado no es un punto núcleo, se marca como ruido (o se deja para ser procesado más tarde si es un punto frontera de otro cluster ya formado).
- Iteración: El proceso se repite con otro punto no visitado hasta que todos los puntos han sido procesados.
DBSCAN es particularmente útil para encontrar clusters complejos en conjuntos de datos ruidosos y no requiere que el usuario especifique el número de clusters de antemano. Sus dos hiperparámetros clave son eps (el radio de búsqueda de vecindad) y MinPts (el número mínimo de puntos para formar un núcleo).
Aprendizaje Global vs. Local:
DBSCAN es un algoritmo de agrupamiento inherentemente local, aunque el resultado final es una partición global de los datos en clusters y ruido.
Aspecto Local: El corazón de DBSCAN reside en la definición de densidad local y la conectividad. Las decisiones sobre si un punto es un núcleo, un frontera o ruido, y si dos puntos pertenecen al mismo clúster, se basan exclusivamente en la densidad de puntos en un vecindario muy localizado definido por el radio \(\epsilon\) y el
MinPts. El algoritmo “expande” los clústeres al moverse de un punto núcleo a sus vecinos, y de estos a sus vecinos, y así sucesivamente. Esta capacidad de crecer y formar clústeres orgánicamente a partir de las densidades locales es lo que permite a DBSCAN descubrir formas arbitrarias y adaptarse a la estructura local de los datos. No hay una función global o centroides predefinidos que guíen la agrupación; todo se deriva de las propiedades de densidad local.Resultado Global (Partición): Aunque el proceso es local, el resultado final es una partición global del conjunto de datos en varios clústeres y un conjunto de puntos de ruido. Una vez que todos los puntos han sido procesados y los clústeres expandidos, se obtiene una vista global de la estructura de agrupamiento.
| Guía rápida para elegir DBSCAN | ||
| Density-Based Spatial Clustering of Applications with Noise (DBSCAN) | ||
| Criterio | Aplica | Detalles |
|---|---|---|
| Fuente: Elaboración propia | ||
Expectation Maximization (EM)
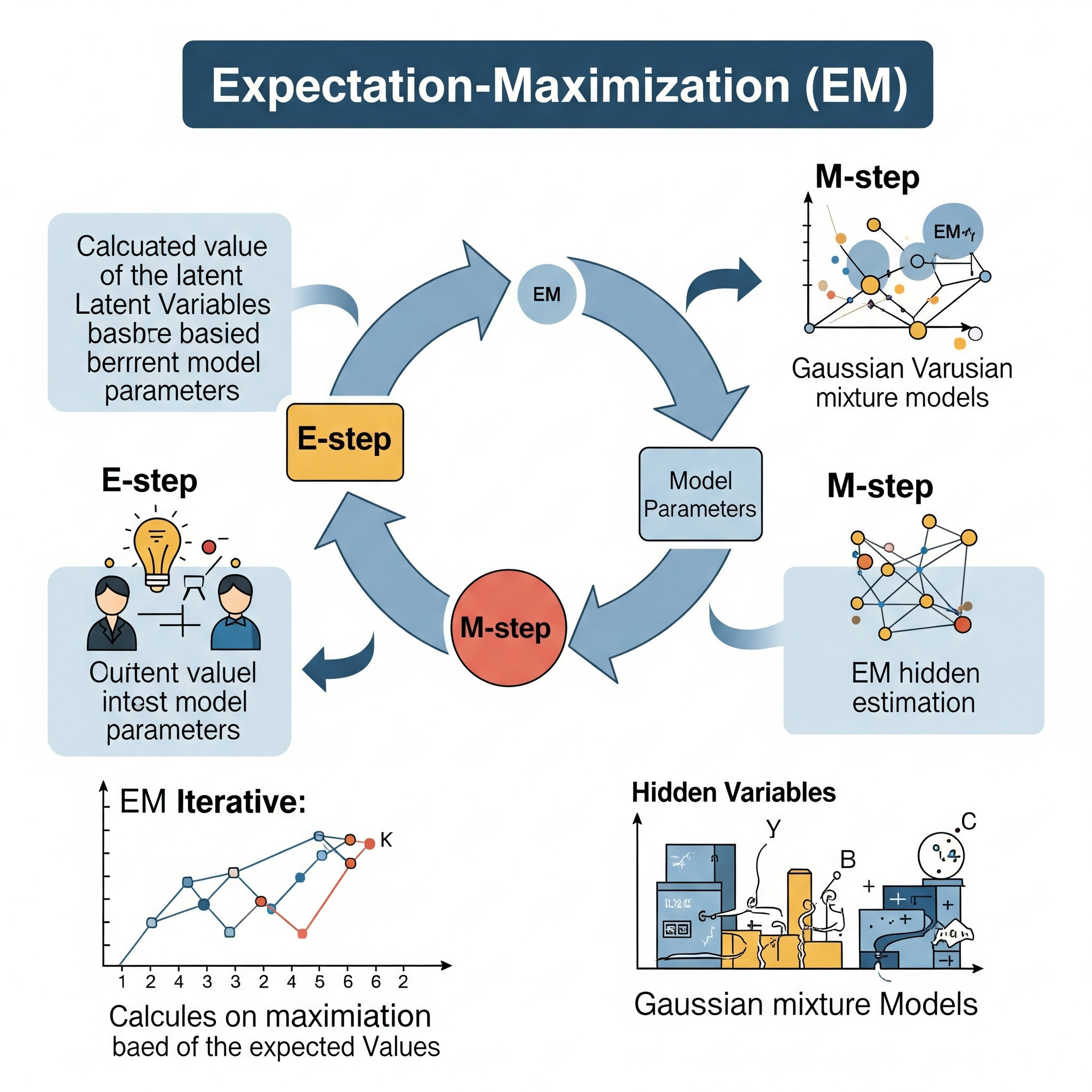
El algoritmo Expectation-Maximization (EM) es un método iterativo utilizado en estadística para encontrar las estimaciones de máxima verosimilitud (MLE) o las estimaciones de máxima a posteriori (MAP) de los parámetros en modelos estadísticos, especialmente cuando el modelo depende de variables latentes (no observadas o “ocultas”) o cuando los datos están “incompletos”.
EM es particularmente útil para modelos de mezcla, donde se asume que los datos observados son una mezcla de varias distribuciones subyacentes, y la pertenencia de cada punto de datos a una distribución específica es la variable latente. El algoritmo consta de dos pasos principales que se alternan hasta la convergencia:
-
Paso E (Expectation Step - Paso de Expectativa):
- En este paso, dadas las estimaciones actuales de los parámetros del modelo, se calculan las probabilidades esperadas (o “responsabilidades”) de que cada punto de datos observado pertenezca a cada una de las componentes latentes (o de que las variables latentes tomen ciertos valores).
- Esencialmente, se está haciendo una “suposición” sobre los valores de las variables latentes basándose en los parámetros actuales del modelo y los datos observados.
-
Paso M (Maximization Step - Paso de Maximización):
- En este paso, utilizando las “responsabilidades” calculadas en el Paso E (tratándolas como si fueran observaciones completas), se re-estiman los parámetros del modelo para maximizar la verosimilitud esperada.
- Esto es típicamente un problema de optimización más simple que el problema original de máxima verosimilitud con datos incompletos. Se ajustan los parámetros (ej., medias, varianzas, pesos de mezcla) para que el modelo se ajuste mejor a los datos, considerando las asignaciones “blandas” a las variables latentes.
Los Pasos E y M se repiten iterativamente. La verosimilitud del modelo está garantizada para no disminuir en cada iteración, y el algoritmo converge a un máximo local de la función de verosimilitud.
Aplicaciones comunes: * Modelos de Mezcla Gaussiana (GMMs): Un uso prototípico del EM para el clustering no supervisado. * Modelos Ocultos de Markov (HMMs): Para problemas de reconocimiento de voz y bioinformática. * Imputación de datos faltantes: Para estimar valores faltantes en un conjunto de datos. * Análisis de componentes latentes.
Aprendizaje Global vs. Local:
El algoritmo Expectation-Maximization (EM) es un método de aprendizaje global, pero es importante entender un matiz sobre su convergencia.
Aspecto Global: EM tiene como objetivo encontrar los parámetros de un modelo probabilístico global (como un GMM completo que describe la distribución de todo el conjunto de datos) que maximicen la verosimilitud de los datos observados. Los parámetros que se estiman (medias, covarianzas, pesos de mezcla en un GMM) son válidos para todo el espacio de características. El algoritmo itera sobre todo el conjunto de datos en cada paso E y M para actualizar estos parámetros globales. La solución que busca EM es una representación unificada y global de las distribuciones subyacentes de los datos.
Convergencia a Máximos Locales: Aunque EM busca una solución global, una limitación crítica es que solo está garantizado para converger a un máximo local de la función de verosimilitud, no necesariamente al máximo global. Esto significa que el resultado final puede depender de la inicialización de los parámetros del modelo. Si la función de verosimilitud tiene múltiples “picos” (máximos locales), EM puede quedar “atrapado” en uno de ellos. Para mitigar esto, es una práctica común ejecutar EM varias veces con diferentes inicializaciones aleatorias y seleccionar el resultado con la verosimilitud más alta.
Por lo tanto, mientras que el objetivo de EM es aprender un modelo global que abarque todo el espacio de datos, su método iterativo de optimización lo hace susceptible a encontrar óptimos locales en la función de verosimilitud. La forma en que un modelo probabilístico como un GMM puede modelar relaciones no lineales en los datos es que, al combinar múltiples distribuciones gaussianas (lineales), el modelo resultante puede capturar formas y densidades complejas y no lineales en el espacio de características. EM es el algoritmo que permite aprender estos componentes subyacentes.
| Guía rápida para elegir EM | ||
| Expectation Maximization (EM) | ||
| Criterio | Aplica | Detalles |
|---|---|---|
| Fuente: Elaboración propia | ||
Hierarchical Clustering (hclust)
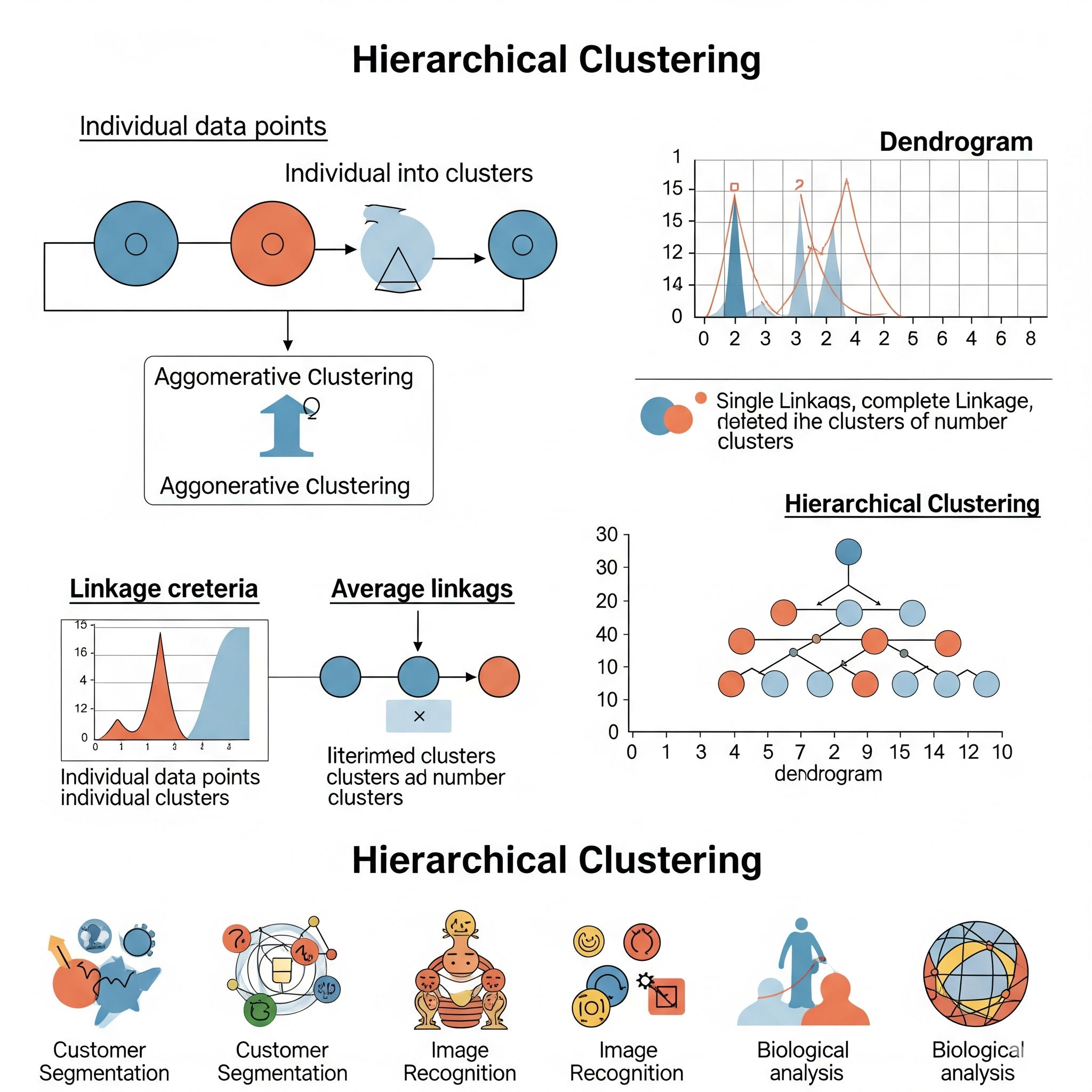
El Agrupamiento Jerárquico (Hierarchical Clustering), a menudo abreviado como hclust, es un método de agrupamiento (clustering) no supervisado que construye una jerarquía de clusters en lugar de una partición plana de los datos (como k-Means). El resultado de un agrupamiento jerárquico se visualiza comúnmente como un dendrograma, un diagrama en forma de árbol que muestra la secuencia de fusiones o divisiones de los clusters.
Existen dos tipos principales de agrupamiento jerárquico:
-
Agrupamiento Aglomerativo (“Bottom-Up”): Es el tipo más común.
- Comienza tratando cada punto de datos como un cluster individual.
- En cada paso, fusiona los dos clusters más cercanos en un nuevo cluster.
- Este proceso continúa hasta que todos los puntos de datos pertenecen a un único cluster grande.
- La “cercanía” entre clusters se define por una métrica de enlace (linkage). Las métricas de enlace comunes incluyen:
- Enlace Único (Single Linkage): Distancia mínima entre dos puntos en diferentes clusters. Tiende a formar clusters “largos” y “delgados”.
- Enlace Completo (Complete Linkage): Distancia máxima entre dos puntos en diferentes clusters. Tiende a formar clusters compactos.
- Enlace Promedio (Average Linkage): Distancia promedio entre todos los pares de puntos en diferentes clusters.
- Método de Ward: Minimiza la varianza total dentro de los clusters después de la fusión. Tiende a formar clusters compactos de tamaño similar.
-
Agrupamiento Divisivo (“Top-Down”):
- Comienza con todos los puntos en un solo cluster grande.
- En cada paso, divide el cluster actual en dos sub-clusters más pequeños.
- Este proceso continúa hasta que cada punto de datos está en su propio cluster individual.
- Es menos común en la práctica debido a su mayor complejidad computacional.
La principal ventaja de hclust es que no requiere especificar el número de clusters de antemano; en cambio, el número de clusters se puede determinar inspeccionando el dendrograma y “cortándolo” a una altura apropiada. También es muy bueno para revelar la estructura anidada de los datos.
Aprendizaje Global vs. Local:
El Agrupamiento Jerárquico (hclust) es un algoritmo que se puede clasificar como de aprendizaje local en su construcción incremental, pero que al final revela una estructura global de los datos.
Aspecto Local (Proceso de Fusión/División): En cada paso del agrupamiento aglomerativo, la decisión de qué clusters fusionar se basa exclusivamente en la distancia (o similitud) entre los clusters más cercanos en ese momento. Esta es una decisión puramente local, ya que solo se consideran los pares de clusters más próximos. El algoritmo construye la jerarquía fusionando iterativamente los vecinos más cercanos, lo que le permite adaptarse a la forma y densidad local de los datos. Las fronteras de los clústeres no están predefinidas por un modelo global; en cambio, emergen de las relaciones de proximidad locales. Esto permite a hclust descubrir clusters de formas arbitrarias y relaciones no lineales que podrían no ser detectadas por métodos que asumen formas específicas de clusters (como k-Means con suposiciones esféricas).
Aspecto Global (Dendrograma): Aunque las decisiones de fusión son locales, el resultado final (el dendrograma) es una representación jerárquica global de las relaciones de todos los puntos de datos. Proporciona una visión completa de cómo todos los puntos se agrupan en diferentes niveles de granularidad, desde clusters individuales hasta un solo cluster grande. Esta estructura global revela patrones de anidamiento y relaciones a diferentes escalas.
| Guía rápida para elegir HClust | ||
| Hierarchical Clustering (hclust) | ||
| Criterio | Aplica | Detalles |
|---|---|---|
| Fuente: Elaboración propia | ||
k-Means
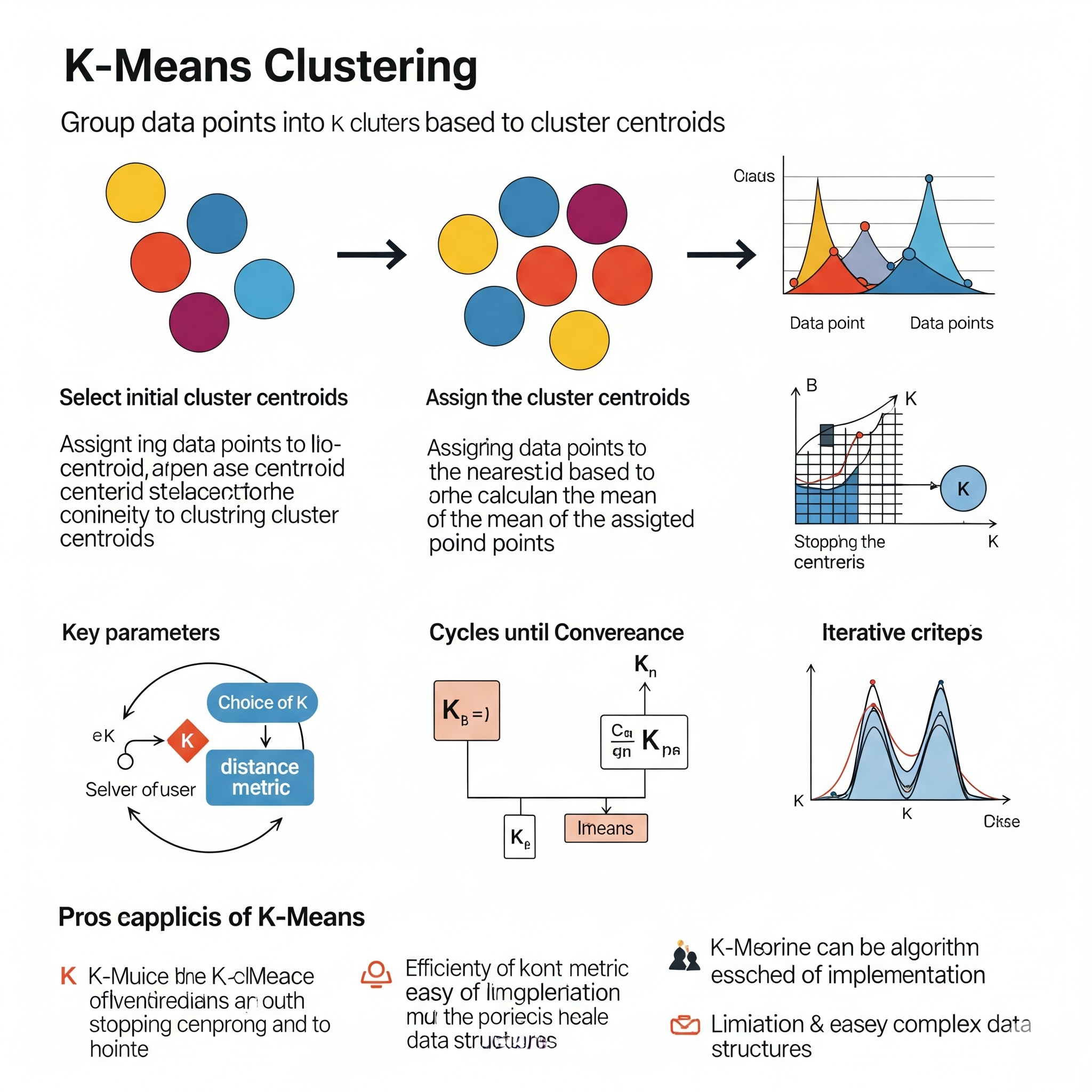
k-Means es uno de los algoritmos de agrupamiento (clustering) no supervisado más populares y ampliamente utilizados. Su objetivo es particionar un conjunto de \(n\) observaciones en \(k\) grupos o “clusters”, donde cada observación pertenece al cluster cuyo centroide (media) es el más cercano.
El algoritmo k-Means opera de la siguiente manera:
-
Inicialización:
- Se elige un número predefinido de clusters, \(k\). Este es un hiperparámetro que debe ser especificado por el usuario.
- Se inicializan \(k\) centroides (puntos centrales de los clusters). Esto se puede hacer de forma aleatoria seleccionando \(k\) puntos de datos al azar como centroides iniciales, o utilizando métodos más sofisticados como k-Means++.
-
Paso de Asignación (Expectation / E-step):
- Para cada punto de datos en el conjunto, se calcula su distancia (comúnmente euclidiana) a cada uno de los \(k\) centroides.
- Cada punto de datos se asigna al cluster cuyo centroide es el más cercano.
-
Paso de Actualización (Maximization / M-step):
- Para cada uno de los \(k\) clusters, se recalcula la posición del centroide como la media (promedio) de todos los puntos de datos que han sido asignados a ese cluster.
-
Iteración:
- Los pasos de Asignación y Actualización se repiten iterativamente.
- El algoritmo converge cuando las asignaciones de los puntos a los clusters ya no cambian, o cuando las posiciones de los centroides no cambian significativamente entre iteraciones.
El objetivo del algoritmo es minimizar la suma de los cuadrados de las distancias de cada punto a su centroide asignado (también conocida como la inercia del cluster o la suma de cuadrados dentro del cluster - WCSS).
Ventajas: Es simple de implementar, computacionalmente eficiente y escalable para grandes conjuntos de datos. Limitaciones: Requiere que el número de clusters \(k\) sea especificado de antemano, es sensible a la inicialización de los centroides, y tiende a formar clusters esféricos de tamaño similar, lo que puede ser una desventaja si los clusters tienen formas arbitrarias o densidades muy diferentes. También es sensible a los outliers.
Aprendizaje Global vs. Local:
k-Means es un modelo de aprendizaje global.
Aspecto Global: k-Means busca una partición global de todo el conjunto de datos en \(k\) clusters. El objetivo de la optimización (minimizar la suma de los cuadrados de las distancias a los centroides) se calcula sobre todos los puntos de datos y todos los clusters simultáneamente. Los centroides, una vez convergidos, representan los “centros” de los clusters en el espacio de características, y estos se utilizan para asignar cualquier nuevo punto a su cluster correspondiente. La solución final es una asignación de cada punto a un cluster que se aplica a nivel global.
Asignaciones Locales dentro de una Optimización Global: Aunque en cada iteración los puntos se asignan a su centroide “local” más cercano, esta asignación es parte de un proceso iterativo que busca optimizar un criterio global (la inercia total del cluster). Los centroides mismos son influenciados por todos los puntos asignados a su cluster, y la reubicación de los centroides afecta las asignaciones de todos los puntos en la siguiente iteración. El resultado son fronteras de decisión lineales (hiperplanos) entre los clusters (cuyas combinaciones pueden formar polígonos de Voronoi), que son una característica de un modelo global que divide el espacio. Si los datos no se distribuyen linealmente y los clusters tienen formas no esféricas o densidades muy diferentes, k-Means puede tener dificultades para descubrirlos, precisamente por su naturaleza global de optimización de la distancia euclidiana a un centroide.
| Guía rápida para elegir k-means | ||
| K - Means | ||
| Criterio | Aplica | Detalles |
|---|---|---|
| Fuente: Elaboración propia | ||
k-Medians
k-Medians es un algoritmo de agrupamiento (clustering) no supervisado que es una variante de k-Means. Al igual que k-Means, su objetivo es particionar un conjunto de \(n\) observaciones en \(k\) grupos o “clusters”. La principal diferencia radica en cómo se calcula el “centro” de cada cluster y la métrica de distancia utilizada en su función de costo.
Mientras que k-Means utiliza la media (mean) de los puntos de un cluster como su centroide y minimiza la suma de los cuadrados de las distancias euclidianas (norma L2), k-Medians utiliza la mediana (median) de los puntos de un cluster como su “centro” y minimiza la suma de las distancias absolutas (norma L1 o distancia de Manhattan).
El algoritmo k-Medians opera de manera muy similar a k-Means:
-
Inicialización:
- Se elige un número predefinido de clusters, \(k\).
- Se inicializan \(k\) medianas (puntos centrales de los clusters), a menudo de forma aleatoria.
-
Paso de Asignación:
- Para cada punto de datos en el conjunto, se calcula su distancia de Manhattan (L1) a cada una de las \(k\) medianas.
- Cada punto de datos se asigna al cluster cuya mediana es la más cercana.
-
Paso de Actualización:
- Para cada uno de los \(k\) clusters, se recalcula la posición de la mediana como la mediana multivariada (componente por componente) de todos los puntos de datos que han sido asignados a ese cluster.
-
Iteración:
- Los pasos de Asignación y Actualización se repiten iterativamente.
- El algoritmo converge cuando las asignaciones de los puntos a los clusters ya no cambian, o cuando las posiciones de las medianas no cambian significativamente.
Ventajas clave de k-Medians sobre k-Means:
- Robustez a Outliers: Al usar la mediana en lugar de la media, k-Medians es significativamente más robusto a los valores atípicos (outliers). Los outliers influyen fuertemente en la media (tirando de ella), pero tienen un impacto mucho menor en la mediana.
- Métrica de Distancia: La distancia L1 es a veces más apropiada que la L2 cuando las diferencias entre las características son más importantes que sus valores al cuadrado, o cuando los datos no son necesariamente continuos o gaussianos.
Limitaciones: * Requiere que el número de clusters \(k\) sea especificado de antemano. * La mediana multivariada puede ser más compleja de calcular que la media. * Puede ser más lento que k-Means en algunos escenarios.
Aprendizaje Global vs. Local:
Al igual que k-Means, k-Medians es un modelo de aprendizaje global.
Aspecto Global: k-Medians busca una partición global de todo el conjunto de datos en \(k\) clusters. El objetivo de la optimización (minimizar la suma de las distancias L1 a las medianas) se calcula sobre todos los puntos de datos y todos los clusters simultáneamente. Las medianas, una vez convergidas, representan los “centros” robustos de los clusters en el espacio de características, y estos se utilizan para asignar cualquier nuevo punto a su cluster correspondiente. La solución final es una asignación de cada punto a un cluster que se aplica a nivel global.
Asignaciones Locales dentro de una Optimización Global: Si bien en cada iteración los puntos se asignan a su mediana “local” más cercana, esta asignación es parte de un proceso iterativo que busca optimizar un criterio global (la suma total de distancias L1). Las medianas mismas son influenciadas por todos los puntos asignados a su cluster, y la reubicación de las medianas afecta las asignaciones de todos los puntos en la siguiente iteración. El resultado son fronteras de decisión lineales (debido al uso de la distancia L1, similar a las fronteras de Voronoi), que son una característica de un modelo global que divide el espacio. Aunque es más robusto a outliers, k-Medians todavía tiende a encontrar clusters que son más o menos “esféricos” o convexos en la métrica L1, y puede tener dificultades con clusters de formas muy arbitrarias o no lineales.
| Guía rápida para elegir k-medians | ||
| K - Medians | ||
| Criterio | Aplica | Detalles |
|---|---|---|
| Fuente: Elaboración propia | ||