🧠 4. Redes Neuronales
Ejemplos: MLP, CNN, RNN, Transformers.
Uso: Perfectas para imágenes (CNN), texto (Transformers) y series temporales (RNN/LSTM), especialmente con grandes volúmenes de datos no estructurados.
Ventajas: Muy poderosas para datos complejos.
Limitaciones: Requieren mucha data y computación, y tienen menor interpretabilidad.
Autoenconder
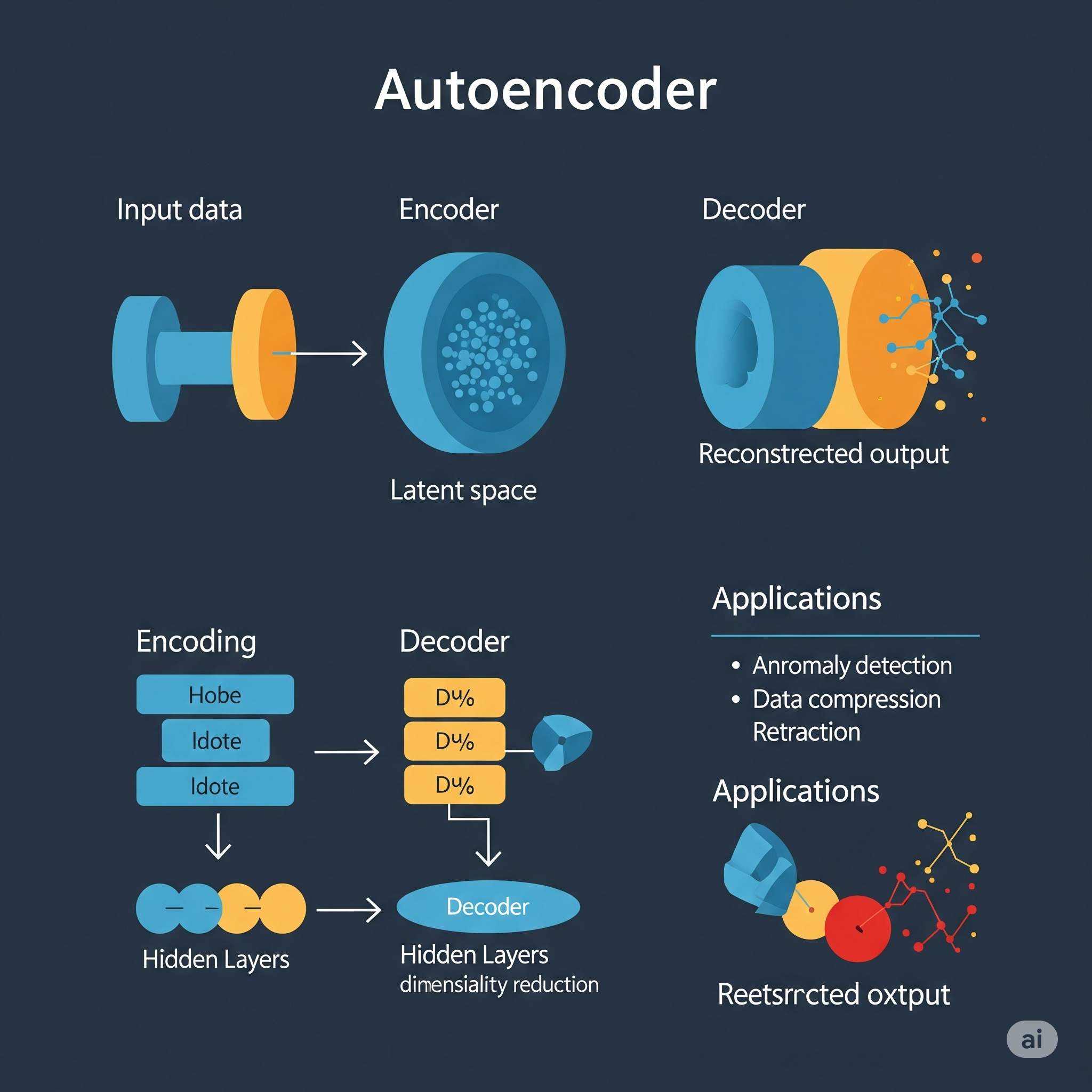
Un Autoencoder es un tipo de red neuronal artificial diseñado para aprender una representación (o codificación) eficiente y comprimida de los datos de entrada, sin supervisión humana. Su objetivo principal es la reducción de dimensionalidad o el aprendizaje de características, lo que lo hace útil para tareas como la detección de anomalías, la denoising de imágenes, o la generación de datos.
La arquitectura básica de un Autoencoder se compone de dos partes principales:
- Encoder (Codificador): Esta parte de la red toma los datos de entrada y los transforma en una representación de menor dimensión, a menudo llamada código, representación latente, o cuello de botella (bottleneck). Es decir, comprime la información esencial de la entrada.
- Decoder (Decodificador): Esta parte toma la representación comprimida (el código) del encoder y la reconstruye de nuevo a la dimensión original de los datos de entrada.
El Autoencoder se entrena para minimizar la diferencia entre la entrada original y su reconstrucción generada por el decoder. Esta diferencia se mide a través de una función de pérdida de reconstrucción (como el error cuadrático medio para datos continuos o la entropía cruzada para datos binarios). Al forzar a la red a reconstruir su propia entrada a partir de una representación comprimida, el Autoencoder aprende las características más salientes y útiles de los datos de forma no supervisada.
Existen varias variantes de Autoencoders, como los Autoencoders Denoising (que aprenden a reconstruir datos limpios a partir de datos con ruido), los Autoencoders Variacionales (VAEs) (que aprenden una distribución probabilística de la representación latente, útiles para la generación de datos), y los Autoencoders Convolucionales (que usan capas convolucionales, ideales para imágenes).
Aprendizaje Global vs. Local:
Un Autoencoder se considera principalmente un modelo de aprendizaje global, aunque con una perspectiva única debido a su naturaleza de compresión y reconstrucción.
Aspecto Global: Un Autoencoder aprende una transformación global de los datos. El encoder aprende a mapear todo el espacio de entrada a un espacio de representación latente, y el decoder aprende a mapear ese espacio latente de vuelta al espacio de salida. Las ponderaciones y sesgos de la red se ajustan para encontrar esta transformación que funciona de manera óptima para todo el conjunto de datos de entrenamiento, permitiendo la reconstrucción más fiel posible en general. La función de pérdida de reconstrucción se minimiza a nivel de todo el conjunto de datos, no solo en vecindarios específicos.
Representación Local vs. Reconstrucción Global: Aunque el objetivo final es una reconstrucción global de la entrada, la representación latente (el código) puede verse como una forma de capturar características o patrones importantes que, en cierto sentido, resumen la información “local” o particular de cada instancia de datos de una manera comprimida. Sin embargo, la forma en que estas características se aprenden y se utilizan para la reconstrucción se rige por un conjunto global de parámetros de la red. No se entrena un modelo separado para cada vecindario de datos, sino una única red que aprende una función de mapeo para todo el dominio.
En resumen, el Autoencoder aprende una representación eficiente y una capacidad de reconstrucción que se aplica de manera consistente a todos los datos, lo que lo clasifica como un modelo de aprendizaje global que busca una solución unificada para el problema de la codificación y decodificación de datos.
| Guía rápida para elegir autoencoder | ||
| Autoenconder | ||
| Criterio | Aplica | Detalles |
|---|---|---|
| Fuente: Elaboración propia | ||
Back - Propagation
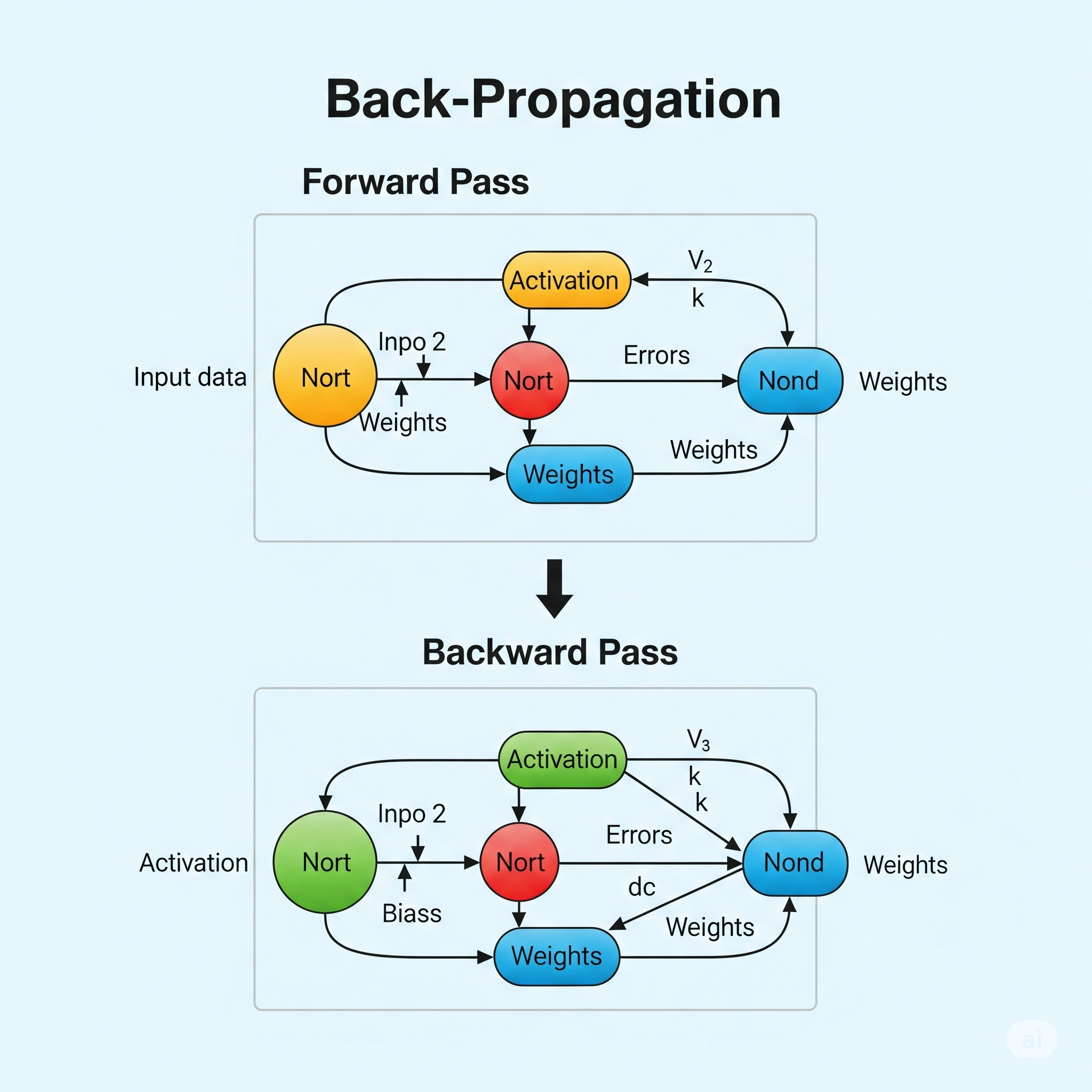
Back-Propagation (Retropropagación) es el algoritmo fundamental de entrenamiento utilizado para ajustar los pesos de las redes neuronales artificiales multicapa (MLP). La idea central de Back-Propagation es calcular la contribución de cada peso al error global de la red y luego ajustar esos pesos para reducir dicho error, propagando la información del error “hacia atrás” desde la capa de salida hasta la capa de entrada.
A diferencia del Perceptron, que solo puede aprender patrones linealmente separables, Back-Propagation permite entrenar redes neuronales profundas con múltiples capas ocultas y funciones de activación no lineales, lo que les permite modelar relaciones complejas y no lineales en los datos.
El funcionamiento de Back-Propagation se divide en dos fases principales que se repiten iterativamente:
-
Fase de Propagación hacia Adelante (Forward Pass):
- Las entradas se pasan a través de la red, desde la capa de entrada, a través de las capas ocultas, hasta la capa de salida.
- En cada neurona, se calcula la suma ponderada de sus entradas (incluido el sesgo) y se aplica la función de activación (ej. sigmoide, tanh, ReLU) para producir la salida de esa neurona.
- La salida final de la red se compara con el valor objetivo real para calcular el error global (o “costo”) de la red, utilizando una función de pérdida (ej. error cuadrático medio para regresión, entropía cruzada para clasificación).
-
Fase de Retropropagación (Backward Pass):
- El error global se propaga hacia atrás desde la capa de salida, a través de las capas ocultas, hasta la capa de entrada.
- En cada capa, se calcula el gradiente del error con respecto a los pesos de las conexiones de esa capa. Esto implica el uso de la regla de la cadena del cálculo diferencial para determinar cuánto contribuye cada peso al error final.
- Una vez calculados los gradientes, los pesos de la red se actualizan en la dirección opuesta al gradiente (es decir, en la dirección de mayor descenso) para reducir el error. Esta actualización se realiza con una tasa de aprendizaje que controla el tamaño del paso. \[w_{ij}^{\text{nuevo}} = w_{ij}^{\text{anterior}} - \alpha \cdot \frac{\partial E}{\partial w_{ij}}\] Donde \(E\) es el error, \(w_{ij}\) es el peso de la conexión entre la neurona \(i\) y la neurona \(j\), y \(\alpha\) es la tasa de aprendizaje.
En el contexto del aprendizaje global vs. local, Back-Propagation es el corazón del entrenamiento de sistemas de aprendizaje global por excelencia (las redes neuronales multicapa). La red neuronal busca aprender una aproximación de función global que mapee las entradas a las salidas, minimizando el error en todo el conjunto de datos. Si los datos no se distribuyen linealmente, Back-Propagation permite que la red aprenda relaciones no lineales complejas a través de sus múltiples capas y funciones de activación no lineales. A diferencia de LOESS o los métodos de regresión ponderada localmente, Back-Propagation no divide explícitamente el problema en múltiples problemas locales independientes para minimizar funciones de costo locales. En cambio, busca minimizar una función de pérdida global para toda la red. Sin embargo, su capacidad para ajustar un gran número de parámetros (pesos) le permite construir representaciones internas de los datos que pueden ser increíblemente flexibles y adaptables, superando la limitación de que “a veces ningún valor de parámetro [en un modelo simple] puede proporcionar una aproximación suficientemente buena”. La retropropagación es lo que permitió a las redes neuronales convertirse en poderosas herramientas de aprendizaje automático.
| Guía rápida para elegir back-propagation | ||
| Back - Propagation | ||
| Criterio | Aplica | Detalles |
|---|---|---|
| Fuente: Elaboración propia | ||
Convolutional Neural Network (CNN)
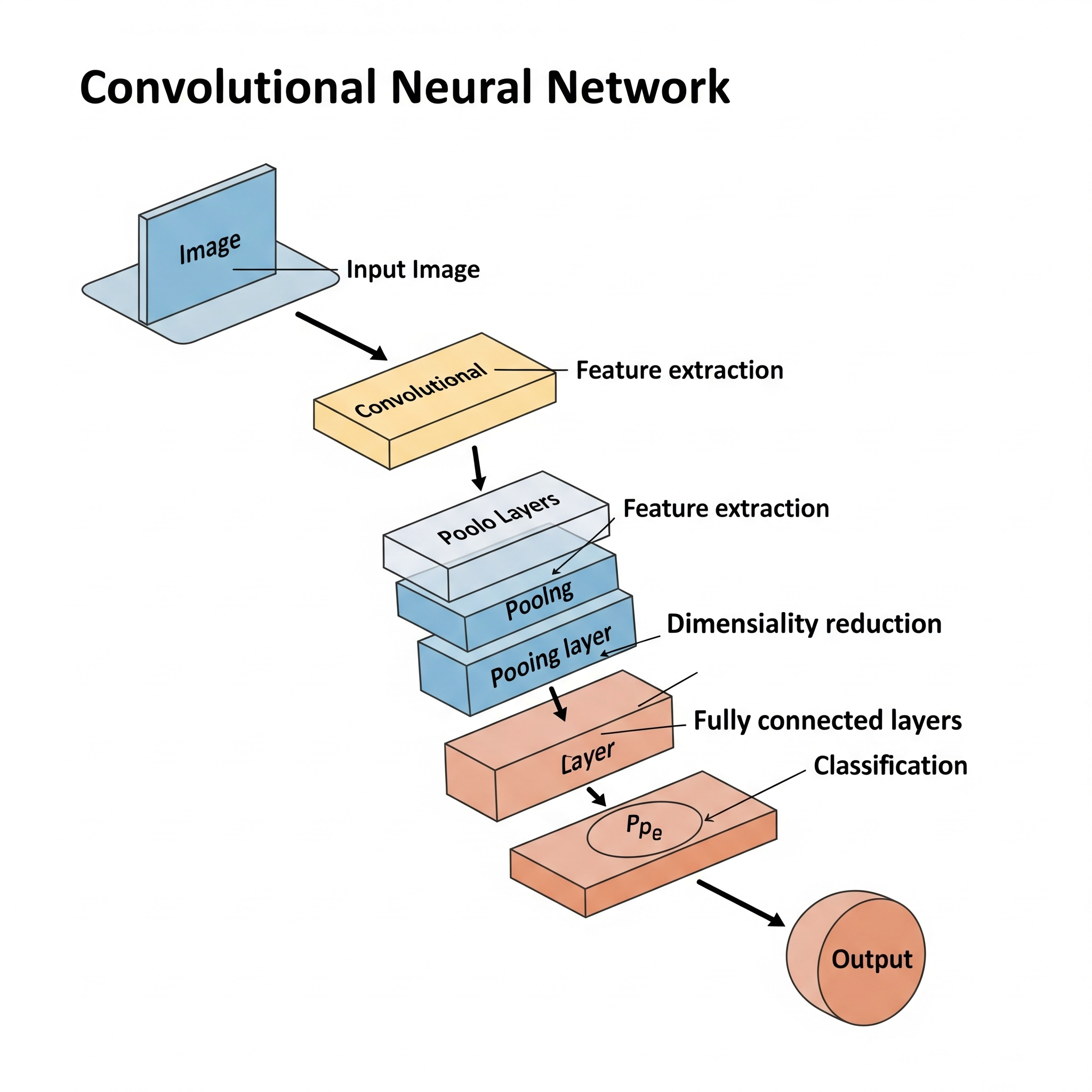
Convolutional Neural Networks (CNNs), también conocidas como ConvNets, son una clase especializada de redes neuronales profundas que han demostrado ser excepcionalmente efectivas en tareas de visión por computadora (como clasificación de imágenes, detección de objetos, reconocimiento facial) y, más recientemente, en procesamiento de lenguaje natural. La idea fundamental de una CNN es imitar el funcionamiento del córtex visual en el cerebro humano, utilizando capas de convolución para detectar automáticamente patrones y características jerárquicas directamente de los datos de entrada sin necesidad de una extracción manual de características.
A diferencia de los Multilayer Perceptrons (MLPs) que conectan cada neurona de una capa con cada neurona de la siguiente capa (lo que resulta en una enorme cantidad de parámetros para datos de alta dimensión como imágenes), las CNNs aprovechan tres ideas arquitectónicas clave:
- Capas de Convolución: Estas capas aplican un pequeño conjunto de filtros (kernels) a la entrada (ej., una imagen). Cada filtro “se desliza” por la entrada (operación de convolución) y calcula un producto punto entre sus valores y los valores de la región de la entrada que está cubriendo. Esto genera un mapa de características que resalta la presencia de patrones específicos (bordes, texturas, formas) en diferentes ubicaciones de la entrada. La ventaja es que los mismos filtros se aplican en múltiples ubicaciones, lo que reduce drásticamente el número de parámetros y captura la localidad de los patrones y la invarianza traslacional.
- Capas de Pooling (Submuestreo): Estas capas se insertan periódicamente entre las capas convolucionales. Su función es reducir la dimensionalidad espacial de los mapas de características (ej., reduciendo el número de píxeles), lo que ayuda a hacer que el modelo sea más robusto a pequeñas variaciones o distorsiones en la posición de las características. Las operaciones comunes son el max pooling (tomar el valor máximo de una región) o el average pooling (tomar el promedio).
- Capas Totalmente Conectadas (Dense): Después de varias capas convolucionales y de pooling, los mapas de características finales se aplanan en un vector y se conectan a una o más capas totalmente conectadas (similares a las de un MLP). Estas capas finales realizan la clasificación o regresión basándose en las características de alto nivel extraídas por las capas anteriores.
El entrenamiento de una CNN se realiza utilizando el algoritmo de Back-Propagation y descenso de gradiente (con sus variantes como SGD, Adam, etc.), ajustando los pesos de los filtros y las conexiones de las capas densas para minimizar una función de pérdida.
En el contexto del aprendizaje global vs. local, las CNNs son un ejemplo sobresaliente de un sistema de aprendizaje global que, en sus capas iniciales, se beneficia de la detección de patrones locales. Cada filtro de convolución aprende a detectar un patrón local específico (un borde vertical, una esquina, etc.) que se repite en diferentes partes de la imagen (lo que es una forma de “regresión ponderada localmente” en el sentido de que el filtro “aplica” su conocimiento local a diferentes ventanas de entrada). Sin embargo, la combinación jerárquica de múltiples capas convolucionales y de pooling, seguida de capas totalmente conectadas, permite que la red construya representaciones cada vez más abstractas y globales del contenido de la imagen. Esto significa que si los datos no se distribuyen linealmente, las CNNs pueden aprender a modelar relaciones extremadamente complejas y no lineales al componer características locales en representaciones globales. La arquitectura de CNNs resuelve la limitación de que “a veces ningún valor de parámetro puede proporcionar una aproximación suficientemente buena” en modelos más simples al permitir que la red aprenda características relevantes de forma automática y jerárquica, adaptándose a las complejidades inherentes de datos como imágenes y videos.
| Guía rápida para elegir CNN | ||
| Convolutional Neural Network (CNN) | ||
| Criterio | Aplica | Detalles |
|---|---|---|
| Fuente: Elaboración propia | ||
Hopfield Network
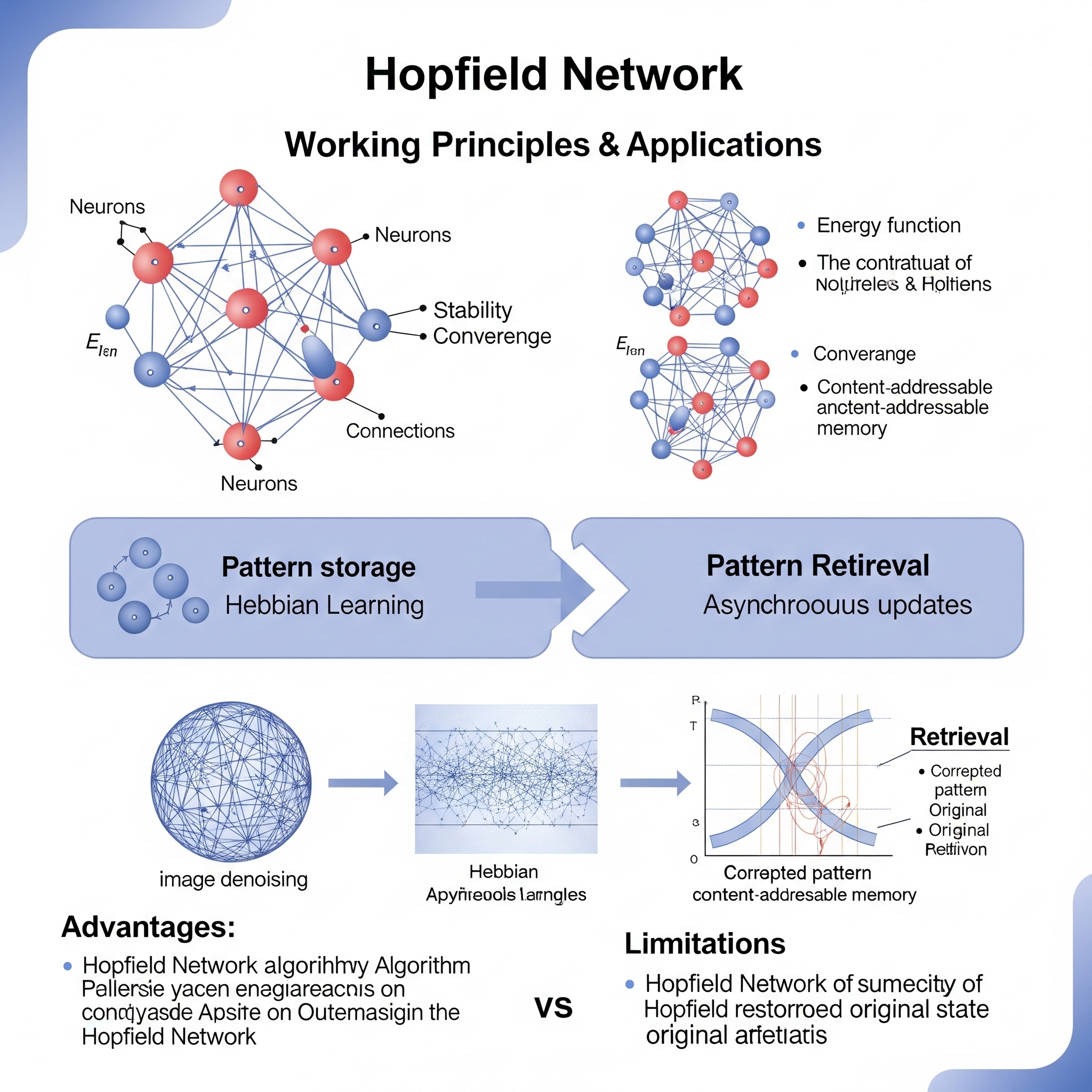
La Red de Hopfield es un tipo de red neuronal recurrente o red neuronal con memoria asociativa, propuesta por John Hopfield en 1982. A diferencia de las redes neuronales de propagación hacia adelante (como el Perceptrón o las MLP entrenadas con Back-Propagation) que se utilizan para el mapeo de entrada a salida, la idea fundamental de una Red de Hopfield es funcionar como un sistema de memoria asociativa y un sistema dinámico que converge a estados estables. Su objetivo principal es almacenar y recuperar patrones binarios, así como resolver problemas de optimización.
El funcionamiento de una Red de Hopfield se basa en los siguientes principios:
- Neuronas Binarias: La red consta de un conjunto de neuronas (nodos) que son binarias, lo que significa que solo pueden tomar dos estados posibles, generalmente \(1\) o \(-1\).
- Conexiones Ponderadas: Cada neurona está conectada a todas las demás neuronas (excepto a sí misma) mediante conexiones simétricas y ponderadas. Los pesos de estas conexiones se calculan de manera que los patrones que se quieren “memorizar” se conviertan en estados de energía mínima de la red. La regla de aprendizaje más común para establecer estos pesos es la regla de Hebb: si dos neuronas se activan juntas para un patrón, el peso entre ellas se incrementa.
- Dinámica de Activación: Cuando se presenta una entrada a la red (que puede ser un patrón ruidoso o incompleto), las neuronas se actualizan de forma asíncrona o síncrona. La activación de cada neurona se recalcula en función de la suma ponderada de las activaciones de las otras neuronas a las que está conectada. \[S_i = \text{sgn}\left(\sum_{j \neq i} W_{ij} S_j\right)\] Donde \(S_i\) es el estado de la neurona \(i\), \(W_{ij}\) es el peso entre la neurona \(i\) y \(j\), y \(\text{sgn}\) es la función signo.
- Convergencia a Estados Estables: Este proceso de actualización se repite hasta que la red alcanza un estado estable (un “atractor”), donde las activaciones de las neuronas ya no cambian. Si la red ha sido entrenada correctamente, este estado estable corresponderá al patrón memorizado más cercano a la entrada inicial (memoria asociativa).
- Función de Energía: La estabilidad de la red se puede describir mediante una función de energía de Lyapunov. Durante la dinámica de la red, la energía de la red siempre disminuye hasta que se alcanza un mínimo local (un patrón memorizado).
En el contexto del aprendizaje global vs. local, la Red de Hopfield es un sistema de aprendizaje global que exhibe un comportamiento de optimización local. La regla de aprendizaje (como la regla de Hebb) establece los pesos de todas las conexiones para que los patrones deseados se conviertan en mínimos de energía en todo el espacio de estados. Es decir, se busca una configuración global de pesos para memorizar un conjunto de patrones. Sin embargo, la dinámica de recuperación de la red es intrínsecamente un proceso de convergencia local: dada una entrada inicial, la red “cae” en el mínimo de energía más cercano, que corresponde al patrón memorizado.
Si los datos no se distribuyen linealmente, la Red de Hopfield no aplica el concepto de regresión (o clasificación) de la misma manera que LOESS o los árboles de decisión. En cambio, funciona como un sistema de memoria y recuperación de patrones no lineales. Puede almacenar y recuperar patrones complejos que no son linealmente separables. La red busca una solución global (un conjunto de pesos) para almacenar los patrones, y luego, en la recuperación, utiliza un proceso de “búsqueda” local en el espacio de energía para converger a un patrón memorizado. Esto aborda la idea de que “a veces ningún valor de parámetro puede proporcionar una aproximación suficientemente buena” en un modelo de regresión lineal, ya que la Red de Hopfield no es un modelo de regresión en sí, sino un sistema dinámico que encuentra estados de equilibrio. Su capacidad para manejar patrones ruidosos o incompletos para recuperar el patrón completo es una de sus principales fortalezas.
| Guía rápida para elegir hopfield network | ||
| Hopfield Network | ||
| Criterio | Aplica | Detalles |
|---|---|---|
| Fuente: Elaboración propia | ||
Multilayer Perceptron (MP)
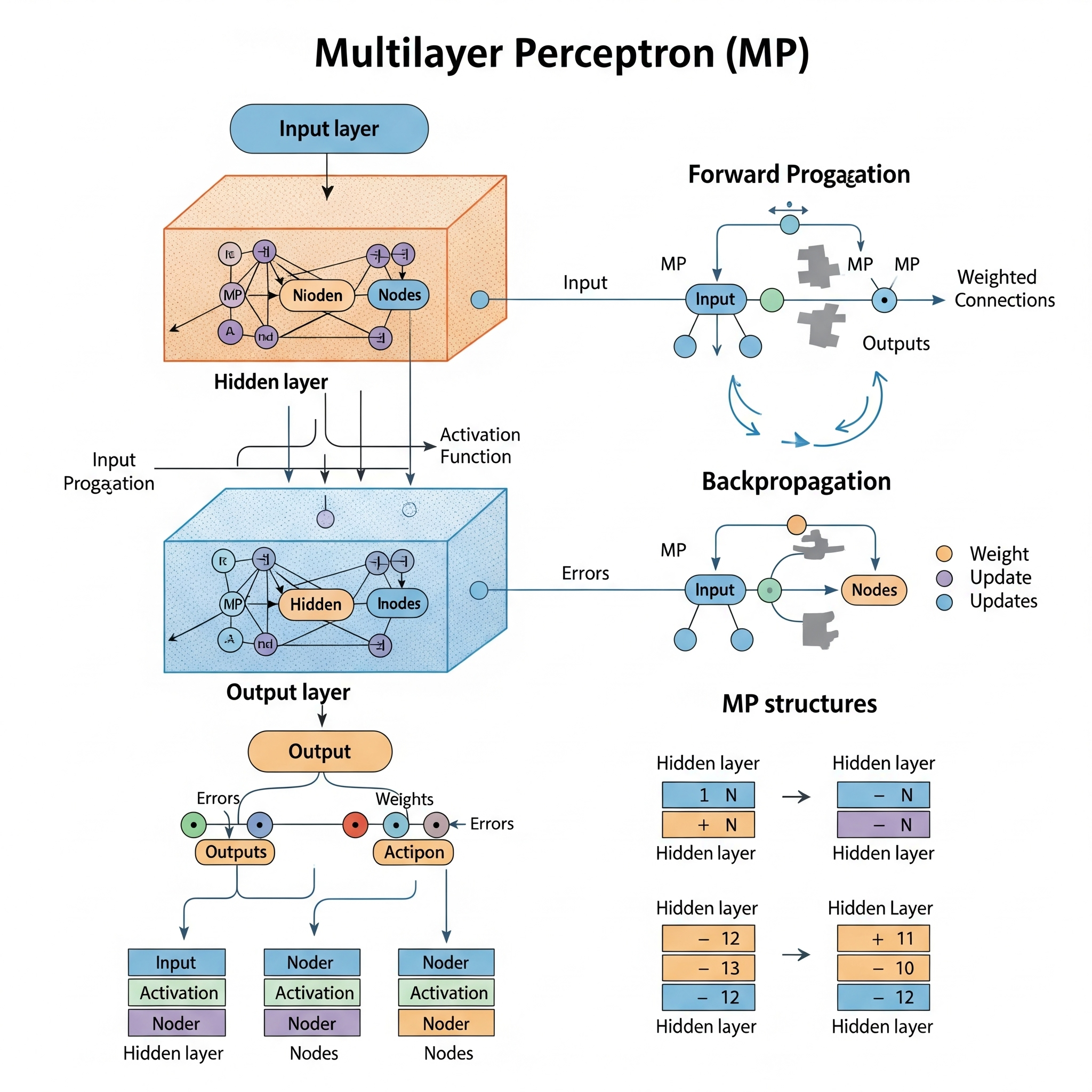
El Multilayer Perceptron (MLP), también conocido como red neuronal de propagación hacia adelante clásica, es un tipo fundamental de red neuronal artificial utilizada para una amplia gama de tareas de aprendizaje supervisado, incluyendo clasificación y regresión. La idea fundamental del MLP es extender el concepto del Perceptrón simple al incorporar una o más capas ocultas entre la capa de entrada y la capa de salida, y utilizando funciones de activación no lineales en estas capas. Esta arquitectura de múltiples capas es lo que le confiere a los MLP su capacidad para aprender y modelar relaciones complejas y no lineales en los datos.
La estructura de un MLP típicamente incluye:
- Capa de Entrada: Recibe las características de entrada del problema.
- Capas Ocultas: Son una o más capas intermedias donde se realizan cálculos complejos. Cada neurona en una capa oculta recibe entradas de la capa anterior, calcula una suma ponderada de estas entradas (más un sesgo), y luego aplica una función de activación no lineal (como la función sigmoide, tanh o ReLU) a esta suma. Es la no linealidad de estas funciones de activación la que permite al MLP aprender relaciones no lineales. \[a_j = f\left(\sum_{i=1}^{n} w_{ij} x_i + b_j\right)\] Donde \(a_j\) es la activación de la neurona \(j\), \(x_i\) son las entradas de la capa anterior, \(w_{ij}\) son los pesos, \(b_j\) es el sesgo, y \(f\) es la función de activación no lineal.
- Capa de Salida: Produce la predicción final de la red. La función de activación en esta capa depende del tipo de problema (ej., una función lineal para regresión, softmax para clasificación multiclase, o sigmoide para clasificación binaria).
El entrenamiento de un MLP se realiza típicamente utilizando el algoritmo de Back-Propagation, que ajusta los pesos de la red de manera iterativa para minimizar una función de pérdida (error) calculada en la capa de salida.
En el contexto del aprendizaje global vs. local, el Multilayer Perceptron es el paradigma de un sistema de aprendizaje global. La red aprende una aproximación de función global que mapea las entradas a las salidas, buscando minimizar la función de pérdida en todo el conjunto de datos de entrenamiento. A diferencia de los sistemas de aprendizaje local que dividen explícitamente el problema global en múltiples problemas más pequeños, el MLP ajusta todos sus pesos de forma interconectada para aprender una representación distribuida de los patrones en los datos. Si los datos no se distribuyen linealmente, el MLP es excepcionalmente capaz de modelar estas relaciones complejas gracias a sus capas ocultas y funciones de activación no lineales. Esto aborda directamente la desventaja de que “a veces ningún valor de parámetro puede proporcionar una aproximación suficientemente buena” en modelos lineales o más simples, ya que el MLP puede construir representaciones internas de gran complejidad para aproximar casi cualquier función continua. Hoy en día, los MLP son la base de muchas arquitecturas de “Deep Learning”.
| Guía rápida para elegir MP | ||
| Multilayer Perceptron (MP) | ||
| Criterio | Aplica | Detalles |
|---|---|---|
| Fuente: Elaboración propia | ||
Perceptron
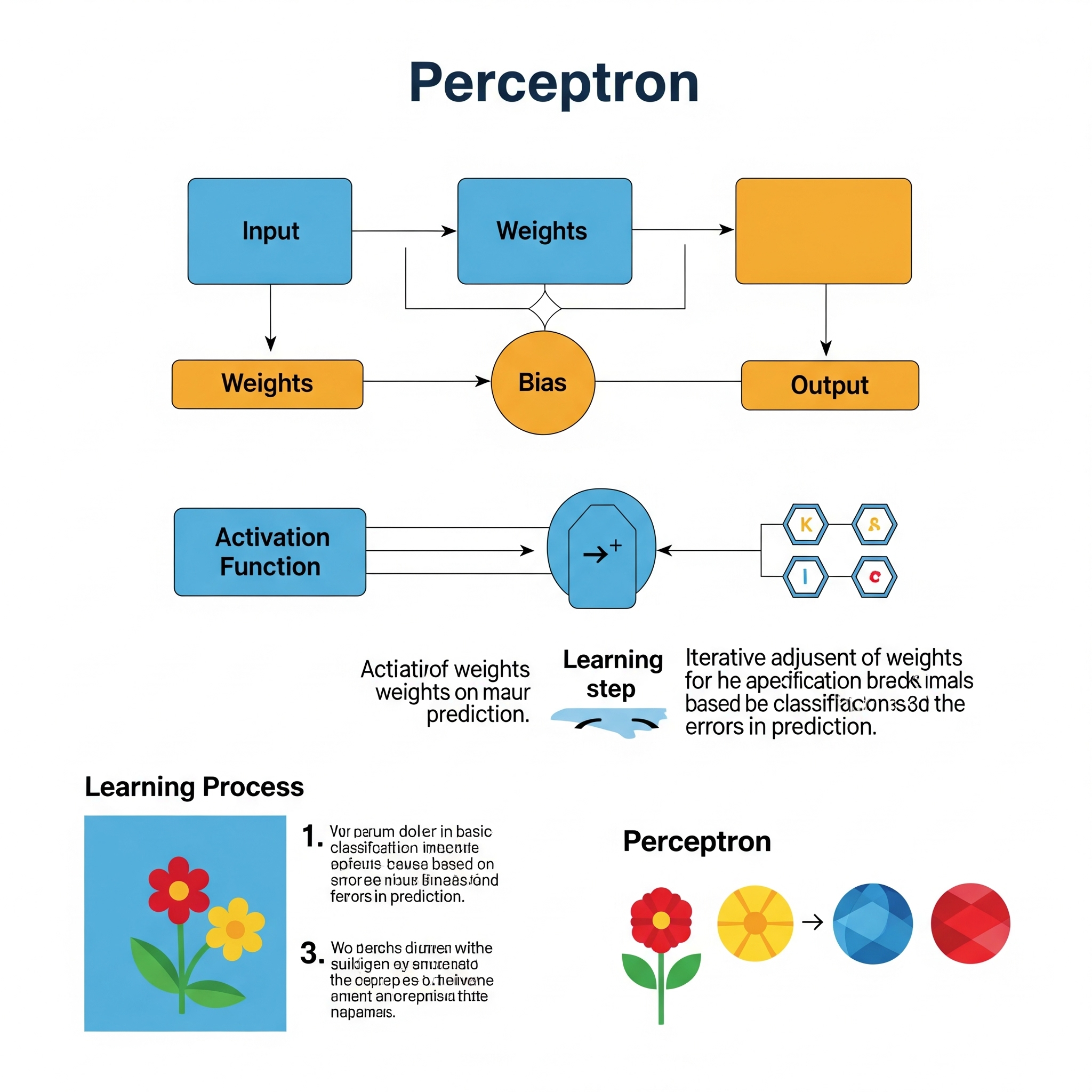
El Perceptron es el algoritmo de aprendizaje supervisado más simple y uno de los primeros modelos de redes neuronales artificiales, propuesto por Frank Rosenblatt en 1957. Está diseñado para tareas de clasificación binaria, es decir, para decidir si una entrada pertenece a una de dos clases posibles. Su idea fundamental es modelar cómo una neurona biológica podría tomar decisiones.
El funcionamiento de un Perceptron es bastante directo:
- Entradas y Pesos: Recibe múltiples entradas (características) y a cada entrada se le asigna un peso. Estos pesos representan la importancia de cada característica.
- Suma Ponderada: Las entradas se multiplican por sus respectivos pesos y se suman. A esta suma se le añade un término de sesgo (bias). \[z = \sum_{i=1}^{n} w_i x_i + b\] Donde \(x_i\) son las entradas, \(w_i\) son los pesos, \(b\) es el sesgo, y \(n\) es el número de entradas.
- Función de Activación: El resultado de la suma ponderada (\(z\)) se pasa a través de una función de activación (generalmente una función escalón o step function). Esta función decide la salida final, que es 1 si la suma excede un umbral (o 0 si no lo excede). Para el Perceptron original, la salida es binaria. \[\text{salida} = \begin{cases} 1 & \text{si } z \geq \text{umbral} \\ 0 & \text{si } z < \text{umbral} \end{cases}\]
- Aprendizaje (Regla de Perceptron): El Perceptron aprende ajustando sus pesos de forma iterativa. Si la predicción es incorrecta, los pesos se actualizan para reducir el error en la siguiente iteración. La regla de actualización de pesos es: \[w_i^{\text{nuevo}} = w_i^{\text{anterior}} + \alpha \cdot (y - \hat{y}) \cdot x_i\] Donde \(\alpha\) es la tasa de aprendizaje, \(y\) es el valor real, y \(\hat{y}\) es la predicción del Perceptron.
En el contexto del aprendizaje global vs. local, el Perceptron es un sistema de aprendizaje global por naturaleza. Busca encontrar un hiperplano de separación lineal único que divida el espacio de características en dos regiones. La idea es que, si los datos son linealmente separables (es decir, si existe una línea, plano o hiperplano que puede separar perfectamente las dos clases), el Perceptron está garantizado para converger y encontrar esa solución.
Sin embargo, precisamente porque busca una solución lineal global, si los datos no se distribuyen linealmente (es decir, no son linealmente separables), el Perceptron no puede encontrar una solución convergente y no puede aprender la relación. Esto ilustra la desventaja de que “a veces ningún valor de parámetro puede proporcionar una aproximación suficientemente buena” cuando se busca una solución global rígida. El Perceptron original no puede aplicar el concepto de regresión ponderada localmente ni adaptarse a complejidades no lineales, a diferencia de modelos posteriores como las redes neuronales multicapa con funciones de activación no lineales o los algoritmos de árboles de decisión. A pesar de esta limitación, el Perceptron sentó las bases para el desarrollo posterior de redes neuronales más complejas.
| Guía rápida para elegir perceptron | ||
| Perceptron | ||
| Criterio | Aplica | Detalles |
|---|---|---|
| Fuente: Elaboración propia | ||
Radial Basis Function Network (RBFN)
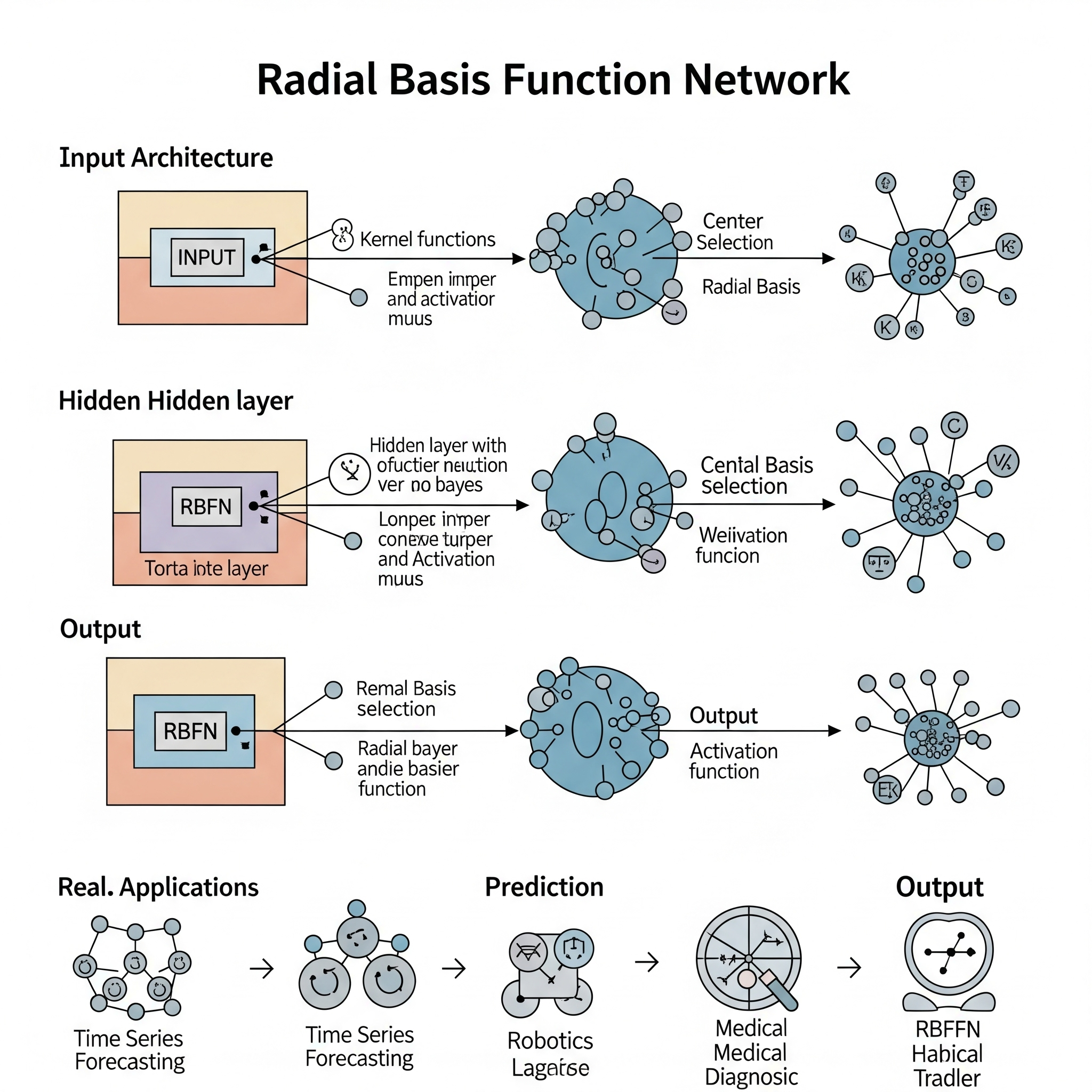
Radial Basis Function Network (RBFN) es un tipo de red neuronal artificial que se utiliza tanto para tareas de clasificación como de regresión. A diferencia de las redes neuronales multicapa perceptrón tradicionales que utilizan funciones de activación sigmoide o ReLU, las RBFN emplean funciones de base radial como sus funciones de activación en la capa oculta. Su estructura es típicamente más simple que un perceptrón multicapa, consistiendo generalmente en tres capas: una capa de entrada, una capa oculta con neuronas de base radial, y una capa de salida.
La idea fundamental de una RBFN radica en su capacidad para modelar relaciones no lineales al mapear datos de entrada a un espacio de características de mayor dimensión donde pueden ser linealmente separables (para clasificación) o donde una función lineal puede aproximar la relación (para regresión). Esto se logra a través de las neuronas de la capa oculta, cada una de las cuales representa un “centro” en el espacio de características.
El funcionamiento de una RBFN implica:
- Capa de Entrada: Recibe las características de entrada.
- Capa Oculta (Neuronas de Base Radial): Cada neurona en esta capa tiene un centro (\(c_i\)) y un radio (o desviación estándar, \(\sigma_i\)). La función de activación de estas neuronas (comúnmente una función Gaussiana) calcula la distancia entre el vector de entrada (\(x\)) y el centro de la neurona (\(c_i\)), y luego aplica la función de base radial. Cuanto más cerca esté la entrada del centro de la neurona, mayor será la activación de esa neurona. \[\phi_i(x) = \exp\left(-\frac{\|x - c_i\|^2}{2\sigma_i^2}\right)\] Donde \(\phi_i(x)\) es la salida de la neurona \(i\), \(\|x - c_i\|\) es la distancia euclidiana entre la entrada \(x\) y el centro \(c_i\), y \(\sigma_i\) es el radio (ancho) de la función Gaussiana.
- Capa de Salida: Las salidas de las neuronas de la capa oculta se combinan linealmente (ponderadas por unos coeficientes, \(w_{ij}\)) para producir la salida final de la red. Para regresión, es una suma ponderada; para clasificación, a menudo se usa una función de activación softmax. \[y_j = \sum_{i=1}^{M} w_{ij}\phi_i(x)\] Donde \(y_j\) es la salida \(j\), \(M\) es el número de neuronas ocultas, y \(w_{ij}\) son los pesos de la capa de salida.
En el contexto del aprendizaje global vs. local, las RBFN son intrínsecamente sistemas de aprendizaje local. Cada neurona de la capa oculta es sensible a una región específica del espacio de entrada, definida por su centro y su radio. La red como un todo es una combinación de estas respuestas locales. Si los datos no se distribuyen linealmente, el concepto de regresión (o clasificación) se aplica de forma muy eficaz mediante esta naturaleza de regresión ponderada localmente. Las RBFN pueden aproximar cualquier función continua con la suficiente cantidad de neuronas de base radial. Esto aborda directamente la desventaja de que “a veces ningún valor de parámetro puede proporcionar una aproximación suficientemente buena” en un solo modelo global, ya que la red puede adaptarse localmente a las características de diferentes regiones del espacio de datos. Son particularmente útiles para problemas de aproximación de funciones, series de tiempo y reconocimiento de patrones.
| Guía rápida para elegir RBFN | ||
| Radial Basis Function Network (RBFN) | ||
| Criterio | Aplica | Detalles |
|---|---|---|
| Fuente: Elaboración propia | ||
Recurrent Neural Networks (RNNs)
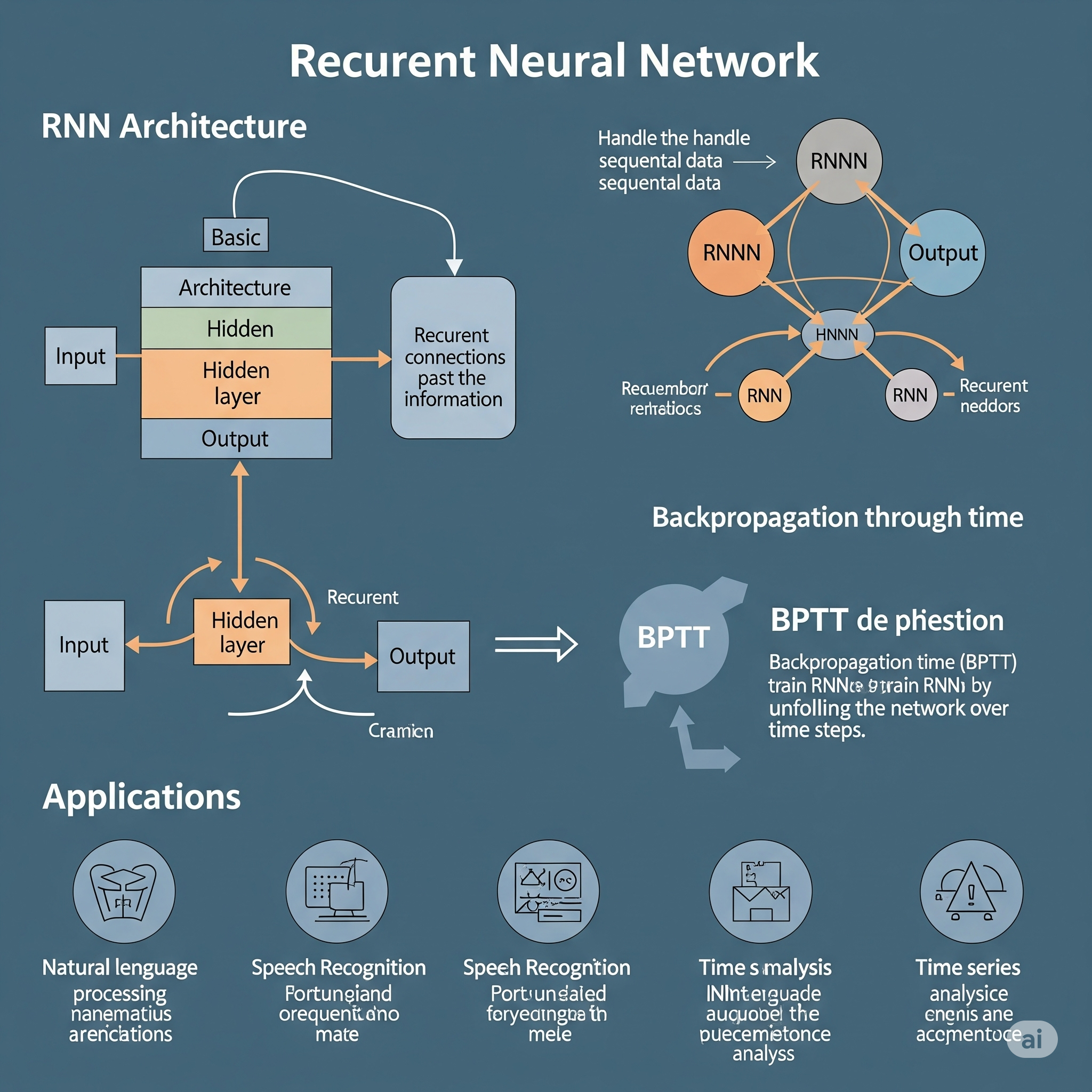
Recurrent Neural Networks (RNNs) son un tipo de red neuronal artificial diseñado específicamente para manejar datos secuenciales o temporales, donde la información de pasos anteriores en la secuencia es relevante para la predicción actual. A diferencia de las redes de propagación hacia adelante (como MLP o CNN) que asumen que las entradas son independientes entre sí, las RNNs tienen “memoria” o conexiones recurrentes que les permiten mantener un estado interno que encapsula información de pasos de tiempo anteriores. Esta característica las hace ideales para tareas como el procesamiento de lenguaje natural (PLN), el reconocimiento de voz, la traducción automática y la predicción de series de tiempo.
La idea fundamental de una RNN es que una unidad recurrente aplica la misma función de transformación a cada elemento de una secuencia, con la particularidad de que la salida de la unidad en un paso de tiempo dado se realimenta como entrada para el mismo proceso en el siguiente paso de tiempo. Esto permite que la red “recuerde” y utilice información pasada al procesar la secuencia actual.
El funcionamiento básico de una RNN en un paso de tiempo (\(t\)) implica:
- Entrada actual (\(x_t\)): El elemento actual de la secuencia.
- Estado oculto anterior (\(h_{t-1}\)): La “memoria” o estado interno de la red del paso de tiempo anterior.
- Cálculo del Estado Oculto Actual (\(h_t\)): Se combina la entrada actual y el estado oculto anterior, y se aplica una función de activación (ej., tanh o ReLU). \[h_t = f(W_{hh} h_{t-1} + W_{xh} x_t + b_h)\] Donde \(W_{hh}\) son los pesos de la conexión recurrente, \(W_{xh}\) son los pesos de la entrada, y \(b_h\) es el sesgo.
- Salida Actual (\(y_t\)): Se genera una salida a partir del estado oculto actual. \[y_t = W_{hy} h_t + b_y\] Donde \(W_{hy}\) son los pesos de la salida y \(b_y\) es el sesgo.
Este proceso de actualización de estado y salida se repite para cada elemento de la secuencia. La “memoria” de la RNN está codificada en el estado oculto que se pasa de un paso de tiempo al siguiente.
El entrenamiento de las RNNs se realiza mediante una variante del algoritmo de Back-Propagation llamada Back-Propagation Through Time (BPTT). BPTT desenrolla la red a lo largo del tiempo, tratando cada paso de tiempo como una capa separada, y luego aplica la retropropagación de manera similar a cómo se entrena un MLP, pero propagando los errores a través de las conexiones recurrentes. Sin embargo, las RNNs simples pueden sufrir de problemas como el desvanecimiento del gradiente (vanishing gradient) o el explosión del gradiente (exploding gradient) para secuencias largas, lo que llevó al desarrollo de arquitecturas más avanzadas como LSTM (Long Short-Term Memory) y GRU (Gated Recurrent Unit).
En el contexto del aprendizaje global vs. local, las RNNs son sistemas de aprendizaje global que están diseñados para aprender y modelar dependencias temporales y patrones secuenciales en un dominio global. A diferencia de los métodos de regresión ponderada localmente como LOESS, que se enfocan en ajustar curvas en regiones específicas de datos, las RNNs intentan aprender una función de mapeo compleja que considera toda la secuencia histórica para producir una predicción. Si los datos (secuenciales) no se distribuyen linealmente, las RNNs son extremadamente efectivas para capturar estas relaciones no lineales y dependencias a largo plazo. Al tener un estado interno que recuerda información pasada, abordan directamente la limitación de que “a veces ningún valor de parámetro puede proporcionar una aproximación suficientemente buena” en modelos estáticos o lineales, ya que pueden adaptar sus predicciones dinámicamente en función del contexto secuencial, lo que las convierte en una herramienta fundamental para el análisis de series de tiempo y el procesamiento de lenguaje.
| Guía rápida para elegir RNN | ||
| Recurrent Neural Networks (RNNs) | ||
| Criterio | Aplica | Detalles |
|---|---|---|
| Fuente: Elaboración propia | ||
Transformers
Los Transformers son una arquitectura de red neuronal profunda que ha revolucionado el campo del Procesamiento de Lenguaje Natural (PLN) y, más recientemente, se ha expandido a la visión por computadora y otras áreas. Introducidos en el artículo “Attention Is All You Need” (Vaswani et al., 2017), la idea fundamental de los Transformers es prescindir de la naturaleza recurrente de las RNNs y las convolucionales de las CNNs, basándose enteramente en un mecanismo llamado auto-atención (self-attention) para capturar dependencias de largo alcance en las secuencias de entrada.
Antes de los Transformers, las RNNs eran el modelo dominante para datos secuenciales. Sin embargo, las RNNs tenían limitaciones como la dificultad para capturar dependencias a muy largo plazo (problema del gradiente desvanecido) y la imposibilidad de paralelizar completamente el procesamiento de secuencias (debido a su naturaleza secuencial). Los Transformers resuelven estos problemas al permitir que cada elemento de la secuencia interactúe directamente con todos los demás elementos de la secuencia, sin importar su distancia.
Los componentes clave de un Transformer incluyen:
Mecanismo de Auto-Atención (Self-Attention): Este es el corazón del Transformer. Para cada token (palabra) en una secuencia, el mecanismo de auto-atención calcula una puntuación de “relevancia” entre ese token y todos los demás tokens de la secuencia. Esto permite que el modelo “pese” la importancia de cada token al generar la representación de otro token. Este proceso se implementa a través de tres vectores para cada token: Query (Q), Key (K) y Value (V). \[\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V\] Donde \(d_k\) es la dimensión de los vectores Key.
Atención Multi-Cabeza (Multi-Head Attention): Para mejorar la capacidad del modelo de enfocarse en diferentes aspectos de la secuencia, el mecanismo de auto-atención se aplica múltiples veces en paralelo con diferentes conjuntos de matrices de pesos (cabezas). Las salidas de estas cabezas se concatenan y se transforman linealmente.
Capas Feed-Forward (Posición por Posición): Después del mecanismo de atención, hay una red neuronal de propagación hacia adelante (un MLP simple) que se aplica de forma independiente a cada posición en la secuencia.
-
Codificador-Decodificador (Encoder-Decoder Architecture): El Transformer original consta de un codificador y un decodificador.
- El codificador toma la secuencia de entrada y genera una representación. Consiste en múltiples capas idénticas, cada una con una capa de auto-atención multi-cabeza y una capa feed-forward.
- El decodificador toma la representación del codificador y genera la secuencia de salida (por ejemplo, la traducción). También consiste en múltiples capas, cada una con auto-atención multi-cabeza, atención multi-cabeza (que atiende a la salida del codificador) y una capa feed-forward.
Codificación Posicional (Positional Encoding): Dado que los Transformers procesan secuencias en paralelo y no tienen una noción inherente de la posición de los tokens (a diferencia de las RNNs), se añade información de la posición de cada token a sus incrustaciones de entrada.
En el contexto del aprendizaje global vs. local, los Transformers son un sistema de aprendizaje global que, gracias a su mecanismo de atención, pueden aprender dependencias a largo alcance y relaciones complejas que son inherentemente globales en la secuencia. Aunque los cálculos individuales de atención pueden verse como una forma de ponderación de la importancia local de los tokens, la red en su conjunto construye una representación global de la secuencia. Si los datos (secuenciales) no se distribuyen linealmente, los Transformers son excepcionalmente capaces de modelar estas relaciones no lineales y dependencias a través de su capacidad para “observar” toda la secuencia a la vez y ponderar la relevancia de cada parte. Esto resuelve de manera fundamental la limitación de que “a veces ningún valor de parámetro puede proporcionar una aproximación suficientemente buena” en modelos secuenciales anteriores, ya que la arquitectura de atención les permite aprender patrones complejos y no lineales en datos secuenciales sin las restricciones de memoria de las RNNs, lo que los convierte en la arquitectura dominante para tareas de PLN avanzadas.
| Guía rápida para elegir transformers | ||
| Transformers | ||
| Criterio | Aplica | Detalles |
|---|---|---|
| Fuente: Elaboración propia | ||