🌟 3. Métodos de Ensamble

Ejemplos: Random Forest, Gradient Boosting (XGBoost, LightGBM, AdaBoost).
Uso: Excelentes para clasificación y regresión en datos tabulares, especialmente en competencias de datos por su alto rendimiento.
Ventajas: Ofrecen alta precisión y son muy robustos.
Limitaciones: Pueden ser difíciles de interpretar y suelen ser computacionalmente más costosos.

---

Adaptive Boosting (AdaBoost)

AdaBoost (Adaptive Boosting) es uno de los algoritmos de boosting más influyentes y el primero en ser propuesto con éxito, desarrollado por Yoav Freund y Robert Schapire en 1995. Es una técnica de aprendizaje conjunto (ensemble learning) utilizada principalmente para clasificación, aunque sus principios pueden extenderse a la regresión. La idea fundamental de AdaBoost es construir un modelo fuerte combinando secuencialmente las predicciones de múltiples clasificadores “débiles” o “base”, y lo hace prestando más atención a los ejemplos que los modelos anteriores clasificaron incorrectamente.

El funcionamiento de AdaBoost se basa en un sistema de re-ponderación de datos en cada iteración:

1. Inicialización de Pesos: Se asigna un peso inicial igual a cada ejemplo de entrenamiento.
2. Entrenamiento del Clasificador Débil: En cada iteración, se entrena un clasificador débil (a menudo un Decision Stump, que es un árbol de decisión de un solo nivel) en el conjunto de datos actual. Este clasificador se enfoca en minimizar el error ponderado.
3. Cálculo del Error Ponderado: Se calcula el error del clasificador débil, teniendo en cuenta los pesos de los ejemplos. Los ejemplos mal clasificados tienen un mayor impacto en este error.
4. Actualización de Pesos de Datos: Los pesos de los ejemplos mal clasificados por el clasificador actual son aumentados, mientras que los pesos de los ejemplos correctamente clasificados son disminuidos. Esto asegura que el siguiente clasificador débil se enfoque más en los ejemplos que son difíciles de clasificar.
5. Cálculo del Peso del Clasificador: Se asigna un peso (o “contribución”) al clasificador débil actual en función de su precisión. Los clasificadores más precisos reciben un peso mayor en la predicción final del conjunto.
6. Combinación de Predicciones: Las predicciones finales del modelo AdaBoost se obtienen mediante una suma ponderada de las predicciones de todos los clasificadores débiles.

En el contexto del aprendizaje global vs. local, AdaBoost es un sistema de aprendizaje global que se construye de manera iterativa a partir de componentes de aprendizaje local. Cada clasificador débil que se entrena en una iteración puede verse como una forma de regresión ponderada localmente (o, más precisamente, clasificación ponderada localmente), ya que ajusta su enfoque basándose en los ejemplos que el modelo combinado anterior no pudo clasificar bien. Al iterar y ajustar los pesos de los datos, AdaBoost se enfoca progresivamente en las regiones del espacio de características donde el modelo actual tiene un rendimiento deficiente. Si los datos no se distribuyen linealmente, el algoritmo aplica el concepto de clasificación (y por extensión, las ideas de regresión) de manera altamente adaptativa. La capacidad de AdaBoost para concentrarse en los “errores” más difíciles aborda directamente la desventaja de que “a veces ningún valor de parámetro puede proporcionar una aproximación suficientemente buena” en un solo modelo. El resultado es un clasificador global muy preciso y robusto, capaz de modelar relaciones complejas y no lineales, que es una combinación ponderada de muchas decisiones locales.

Guía rápida para elegir adaboost
AdaBoost
Criterio	Aplica	Detalles
Tipo de modelo	✅ Supervisado	Ensamble supervisado que combina varios modelos débiles (ej. árboles simples) ajustando pesos según errores anteriores.
Variable respuesta	✅ Categórica (clasificación) o Continua (regresión adaptada)	En clasificación ajusta pesos para mal clasificados; en regresión, adapta predicción por minimización de pérdida.
Variables predictoras	✅ Numéricas y categóricas (requiere codificación para algunas implementaciones)	Puede trabajar con datos mixtos; para variables categóricas suele usar codificación de dummies.
Relación entre variables	✅ Captura no linealidades e interacciones mediante reponderación iterativa	Cada iteración repondera observaciones difíciles, enfocándose en patrones que previos modelos no capturaron.
Normalidad de residuos	❌ No requiere supuestos de normalidad en los residuos	No impone distribución de errores; se basa en función de pérdida, no en supuestos paramétricos.
Independencia de errores	✅ Deseable, aunque no obligatorio (mejor si instancias independientes)	Funciona mejor si cada observación es independiente; sensible a dependencias temporales si no se corrige.
Homoscedasticidad	❌ No asume homoscedasticidad	No requiere varianza constante, ya que funciona sobre el error iterativo en lugar de residuos tradicionales.
Sensible a outliers	⚠️ Moderadamente (outliers pueden obtener demasiado peso durante iteraciones)	Outliers difíciles de clasificar tienden a recibir mayor peso, lo que puede sesgar el ensamble si no se controla el learning rate.
Multicolinealidad entre predictores	✅ Robusto (reduce colinealidad al iterar sobre subconjuntos ponderados)	La reponderación de muestras atenúa el efecto de predictores correlacionados, pues cada iteración puede focalizarse en subconjuntos distintos.
Interpretabilidad	⚠️ Baja (modelo resultante es especie de ’caja negra’)	Es complejo desentrañar la contribución de cada modelo débil; se pueden usar métricas de importancia o SHAP para interpretación.
Velocidad y eficiencia	⚠️ Lento con muchas iteraciones o datos grandes	Cada iteración entrena un modelo débil; muchas iteraciones o modelos complejos pueden ralentizar el entrenamiento.
Validación cruzada	✅ Recomendable para ajustar tasa de aprendizaje y número de iteraciones	K-fold o repeated CV ayudan a elegir tasa de aprendizaje (learning rate) y número de iteraciones (trials).
No funciona bien si...	❌ No es ideal con datos muy ruidosos o clases extremadamente desbalanceadas sin técnicas adicionales	No conviene con instancias altamente ruidosas: se puede sobreajustar rápidamente si la tasa de aprendizaje es alta o no se regula iteraciones.
Fuente: Elaboración propia

Boosting

Boosting es una técnica de aprendizaje conjunto (ensemble learning) que busca transformar un conjunto de modelos “débiles” o “base” en un modelo “fuerte” o “preciso”. La idea fundamental es construir modelos de forma secuencial e iterativa, donde cada nuevo modelo se centra en corregir los errores o deficiencias de los modelos construidos en las iteraciones anteriores. A diferencia del bagging (como en Random Forest), donde los modelos se entrenan de forma independiente, el boosting es intrínsecamente secuencial y adaptativo.

El concepto clave de Boosting radica en la asignación de pesos o en el enfoque en los errores residuales:

1. Iteraciones Secuenciales: El proceso comienza con un modelo base inicial (a menudo simple, como un decision stump).
2. Enfoque en los Errores: En cada iteración subsiguiente, el algoritmo presta más atención a los ejemplos que fueron clasificados (o predichos) incorrectamente por los modelos anteriores, o a los errores residuales no explicados. Esto se logra ya sea re-ponderando los datos (dando más peso a los ejemplos mal clasificados) o ajustando el nuevo modelo para que prediga los residuos de los modelos anteriores.
3. Combinación Ponderada: Las predicciones de todos los modelos débiles se combinan, generalmente a través de una suma ponderada, donde los modelos más precisos reciben un mayor peso en la predicción final.

La fuerza del boosting radica en su capacidad para reducir el sesgo y la varianza del modelo final, al construir un modelo complejo a partir de componentes simples que se complementan entre sí.

En el contexto del aprendizaje global vs. local, Boosting es una estrategia de aprendizaje global que opera construyendo una serie de aproximaciones locales. Cada modelo “débil” que se entrena en una iteración puede verse como una forma de regresión ponderada localmente (o clasificación ponderada localmente), ya que se enfoca en una parte específica del espacio de las características o en los datos con mayor error. El proceso iterativo de Boosting busca corregir estos errores localizados. Si los datos no se distribuyen linealmente, el boosting permite que el concepto de regresión (o clasificación) se aplique de manera muy flexible y potente. La capacidad de concentrarse en los “errores” residuales aborda directamente la desventaja de que “a veces ningún valor de parámetro puede proporcionar una aproximación suficientemente buena” en un solo modelo. Al ensamblar muchos modelos débiles que se adaptan a los errores de los anteriores, Boosting construye un modelo final que es una aproximación de función global altamente adaptable y precisa. Algoritmos como AdaBoost y Gradient Boosting Machines (GBM) son ejemplos prominentes de esta técnica.

Guía rápida para elegir Boosting
Boosting
Criterio	Aplica	Detalles
Tipo de modelo	✅ Supervisado	Ensamble supervisado que combina varios modelos débiles (ej. árboles pequeños) de forma secuencial
Variable respuesta	✅ Categórica (clasificación) o Continua (regresión)	En clasificación se usan votaciones ponderadas; en regresión se suman predicciones graduadas
Variables predictoras	✅ Numéricas y categóricas (requiere codificación para algunas implementaciones)	Acepta variables mixtas; algunas bibliotecas requieren convertir categóricas en dummies
Relación entre variables	✅ Captura no linealidades e interacciones complejas mediante aprendizaje secuencial	Construye modelos débiles en cada iteración, enfocándose en muestras mal clasificadas o con alto residuo
Normalidad de residuos	❌ No requiere supuestos de normalidad	No exige distribución de errores, ya que se basa en función de pérdida sin supuestos paramétricos
Independencia de errores	✅ Deseable, aunque no obligatorio para muchos algoritmos	Mejor si los ejemplos son independientes; puede usar técnicas especiales para datos correlacionados
Homoscedasticidad	❌ No se asume homoscedasticidad	No asume varianza constante, usa función de pérdida directa para optimizar
Sensible a outliers	⚠️ Moderadamente (puede ajustar demasiado a outliers si no se controla)	Los outliers pueden recibir peso excesivo en iteraciones posteriores, por lo que es necesario regularizar o usar robust loss
Multicolinealidad entre predictores	✅ Robusto (cada iteración utiliza un subconjunto ponderado de datos)	La selección de variables se hace implícitamente, reduciendo el impacto de colinealidad
Interpretabilidad	⚠️ Baja (modelo en su conjunto es tipo caja negra)	Difícil de interpretar directamente; se pueden usar métricas de importancia, SHAP o partial dependence para explicación
Velocidad y eficiencia	⚠️ Lento con muchos árboles o altas iteraciones	Cada iteración entrena un modelo débil, por lo que puede ser costoso si el número de iteraciones es alto
Validación cruzada	✅ Recomendable con k-fold o repeated CV para ajustar tasa de aprendizaje y número de iteraciones	CV ayuda a determinar la tasa de aprendizaje (learning rate), número de iteraciones y complejidad de base learners
No funciona bien si...	❌ Si se tienen pocos datos, alto ruido o target muy desbalanceado sin ajuste	No es adecuado si hay muy pocos ejemplos, alta dimensionalidad con poco señal o target extremadamente desequilibrado
Fuente: Elaboración propia

Bootstrapped Aggregation (Bagging)

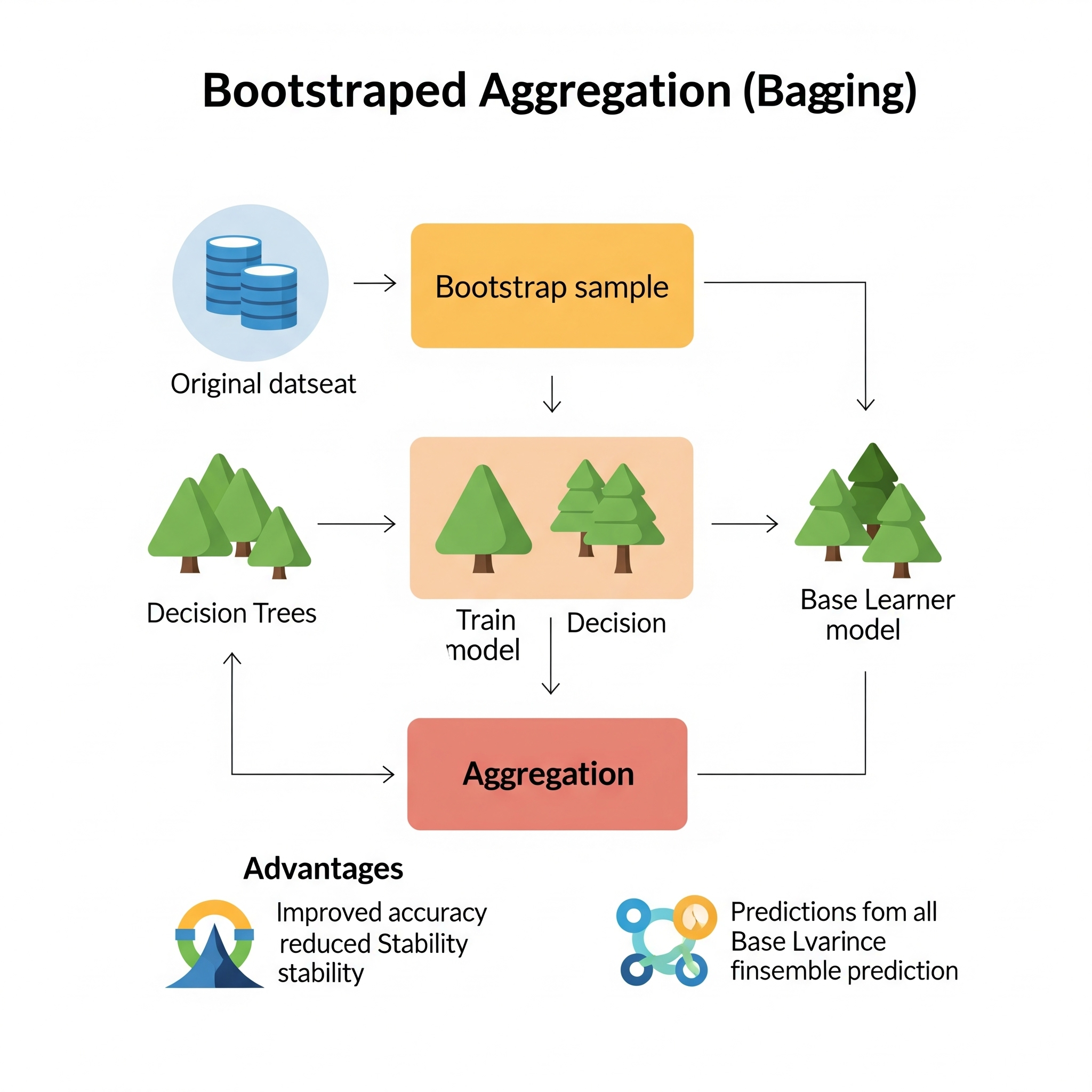
Bootstrapped Aggregation (Bagging) es una técnica de aprendizaje conjunto (ensemble learning) diseñada para mejorar la estabilidad y precisión de los algoritmos de aprendizaje automático, particularmente para reducir la varianza en los modelos. Fue introducida por Leo Breiman en 1996 y es la base de algoritmos muy populares como Random Forest. La idea fundamental de Bagging es entrenar múltiples versiones de un mismo modelo base en diferentes subconjuntos del conjunto de datos original y luego combinar sus predicciones.

El proceso central de Bagging implica dos pasos clave:

1. Muestreo Bootstrap: En lugar de entrenar un único modelo en todo el conjunto de datos de entrenamiento, Bagging crea múltiples conjuntos de datos de arranque (bootstrap samples). Cada muestra de arranque se crea seleccionando aleatoriamente, con reemplazo, un número de observaciones igual al tamaño del conjunto de datos original. Esto significa que algunos puntos de datos pueden aparecer varias veces en una muestra de arranque, mientras que otros pueden no aparecer en absoluto. Este muestreo aleatorio introduce diversidad entre los conjuntos de entrenamiento para cada modelo.

2. Agregación (Aggregation): Una vez que se han entrenado múltiples modelos base independientes (por ejemplo, árboles de decisión) en cada una de estas muestras de arranque, sus predicciones se combinan. Para tareas de clasificación, la combinación se realiza mediante votación por mayoría (la clase más votada). Para tareas de regresión, las predicciones se promedian. Esta agregación de predicciones de modelos diversos reduce la varianza y, por lo tanto, hace que el modelo final sea más robusto y menos propenso al sobreajuste que un solo modelo entrenado en todo el conjunto de datos.

En el contexto del aprendizaje global vs. local, Bagging es una estrategia que combina las ventajas de los modelos de aprendizaje local para construir una aproximación de función global más estable. Cada modelo base (ej. un árbol de decisión) que se entrena en una muestra de arranque puede considerarse un sistema de aprendizaje local, ya que toma decisiones basadas en el subconjunto de datos que le ha sido asignado. Sin embargo, al entrenar estos múltiples modelos en paralelo y luego agregarlos, Bagging construye un modelo final que es una aproximación de función global altamente adaptable. La ventaja principal es que, si los datos no se distribuyen linealmente, el concepto de regresión (o clasificación) se puede aplicar eficazmente mediante esta forma de regresión ponderada localmente (donde los “pesos” son implícitos a través de la agregación de predicciones de modelos entrenados en subconjuntos aleatorios de datos). Bagging aborda el problema de que “a veces ningún valor de parámetro puede proporcionar una aproximación suficientemente buena” en un solo modelo al promediar o votar las predicciones de múltiples modelos, lo que reduce la varianza y mejora la generalización.

Guía rápida para elegir bagging
Bootstrapped Aggregation (Bagging)
Criterio	Aplica	Detalles
Tipo de modelo	✅ Supervisado	Ensamble supervisado que ajusta varios modelos (usualmente árboles) sobre muestras bootstrap y promedia predicciones.
Variable respuesta	✅ Categórica o Continua	En clasificación predice la clase más votada; en regresión, promedia los valores predichos.
Variables predictoras	✅ Numéricas y categóricas	Acepta todo tipo de variables; las categóricas deben codificarse adecuadamente.
Relación entre variables	✅ Captura relaciones no lineales al promediar múltiples modelos	Al promediar múltiples modelos, reduce varianza y captura no linealidades implícitamente.
Normalidad de residuos	❌ No requiere	No impone supuestos sobre la distribución de errores.
Independencia de errores	✅ Deseable, pero no obligatorio	Los datos deben ser independientes; funciona peor en datos con fuerte autocorrelación sin ajuste.
Homoscedasticidad	❌ No se asume homoscedasticidad	No requiere varianza constante puesto que se basa en agregación de múltiples predicciones.
Sensible a outliers	✅ Robusto (cada bootstrap reduce el impacto de outliers)	Cada muestra bootstrap y árbol es menos sensible a valores extremos; la agregación aumenta robustez.
Multicolinealidad entre predictores	✅ Robusto (la agregación mitiga colinealidad)	La selección aleatoria de subconjuntos y bootstrap reduce el efecto de predictores correlacionados.
Interpretabilidad	⚠️ Moderada (difícil interpretar conjunto de modelos)	El modelo final es un conjunto de muchos árboles, lo que dificulta su explicación directa.
Velocidad y eficiencia	⚠️ Moderado (depende del número de árboles y tamaño del dataset)	Entrenar cientos de árboles toma tiempo, pero es paralelizable; la predicción es relativamente rápida.
Validación cruzada	✅ Recomendable usar k-fold	CV ayuda a ajustar parámetros como número de árboles y profundidad máxima de cada árbol.
No funciona bien si...	❌ No es ideal con muy pocos datos o si los base learners son demasiado simples	Con pocos ejemplos, los bootstrap no aportan diversidad suficiente; si los base learners son muy simples, no capturan bien patrones complejos.
Fuente: Elaboración propia

CatBoost

Extreme Gradient Boosting (XGBoost)

XGBoost (Extreme Gradient Boosting) es una implementación optimizada y altamente eficiente del algoritmo de Gradient Boosting Machines (GBM), ampliamente reconocida por su velocidad, rendimiento y escalabilidad en problemas de clasificación y regresión. Ganó una inmensa popularidad debido a su éxito en numerosas competiciones de machine learning (como Kaggle). Aunque se basa en los principios de GBM, XGBoost introduce varias mejoras clave que lo hacen superior en muchos escenarios.

La idea fundamental de XGBoost, al igual que GBM, es construir un modelo aditivo de forma secuencial, donde cada nuevo árbol intenta corregir los errores residuales del conjunto de árboles previos. Sin embargo, XGBoost optimiza este proceso con las siguientes características:

1. Paralelización: Aunque el boosting es inherentemente secuencial, XGBoost permite la paralelización de la construcción de los árboles individuales. Por ejemplo, en el paso de búsqueda de la mejor división, puede evaluar las posibles divisiones en paralelo a través de múltiples núcleos de CPU.
2. Regularización: Incorpora términos de regularización L1 (Lasso) y L2 (Ridge) en la función de costo para controlar la complejidad del modelo y evitar el sobreajuste. Esto es crucial para la generalización.
3. Manejo de Valores Faltantes: Tiene una capacidad incorporada para manejar valores faltantes en los datos, permitiendo al algoritmo aprender la mejor dirección para los valores ausentes.
4. Poda por Profundidad (Depth-First Search): A diferencia de muchos algoritmos de árboles que crecen nivel por nivel, XGBoost puede usar un enfoque de poda por profundidad, lo que a menudo resulta en árboles más eficientes.
5. Caché-Aware Computing: Optimiza el acceso a la memoria para manejar grandes conjuntos de datos de manera eficiente.
6. Flexibilidad de Función de Pérdida: Permite el uso de funciones de pérdida personalizadas, lo que lo hace adaptable a una amplia gama de problemas.

En el contexto del aprendizaje global vs. local, XGBoost es una poderosa estrategia de aprendizaje global que se construye iterativamente a partir de componentes de aprendizaje local. Cada árbol de regresión (o clasificación) individual es un “aprendiz débil” que se enfoca en las deficiencias del modelo acumulado. Si los datos no se distribuyen linealmente, el algoritmo aplica el concepto de regresión (o clasificación) de manera altamente sofisticada mediante esta regresión ponderada localmente. Al centrarse en los errores residuales y optimizar el proceso de manera rigurosa, XGBoost aborda de manera excepcional la desventaja de que “a veces ningún valor de parámetro puede proporcionar una aproximación suficientemente buena” en un solo modelo. Su combinación de precisión, velocidad y capacidad para manejar grandes conjuntos de datos lo ha convertido en uno de los algoritmos más populares y efectivos en la práctica del machine learning.

Guía rápida para elegir xgboost
XGBoost
Criterio	Aplica	Detalles
Tipo de modelo	✅ Supervisado	Ensamble supervisado que combina múltiples árboles débiles optimizados con gradiente descendente acelerado.
Variable respuesta	✅ Continua (regresión) o Categórica (clasificación)	En regresión predice valores continuos; en clasificación combina probabilidades o clases mediante log-loss o multiclass objectives.
Variables predictoras	✅ Numéricas y categóricas (requiere codificación para dummies o label encoding)	Acepta variables mixtas; las categóricas deben convertirse a formatos compatibles (p. ej. factor numerico, one-hot encoding).
Relación entre variables	✅ Captura no linealidades e interacciones complejas vía árboles en boosting	Cada iteración ajusta un nuevo árbol enfocándose en los residuos del modelo anterior, capturando patrones complejos.
Normalidad de residuos	❌ No requiere supuestos de normalidad	No impone distribución paramétrica de errores, ya que optimiza funciones de pérdida directamente.
Independencia de errores	✅ Deseable, aunque no obligatorio (mejor si instancias independientes)	Funciona mejor si cada muestra es independiente; sensible a series de tiempo sin preparación apropiada.
Homoscedasticidad	❌ No asume homoscedasticidad	No requiere varianza constante, porque basa la optimización en gradientes del loss, no en supuestos de error.
Sensible a outliers	⚠️ Moderadamente (puede sobreajustar a outliers si no regula)	Los outliers difíciles de predecir pueden recibir demasiado peso en iteraciones sucesivas; usar _learning_rate_ bajo y _max_depth_ pequeño para regular.
Multicolinealidad entre predictores	✅ Robusto (reduce efecto de colinealidad al usar árboles secuenciales)	Los árboles reducen el impacto de variables altamente correlacionadas, aunque múltiples iteraciones pueden aún privilegiar características correlacionadas.
Interpretabilidad	⚠️ Baja (modelo complejo y tipo ’caja negra’)	Difícil interpretar directamente cada árbol; se utilizan métricas de importancia, SHAP values o partial dependence plots para explicación.
Velocidad y eficiencia	✅ Muy rápido y escalable (implementación optimizada, paralelizable)	Implementación en C++ altamente optimizada (CPU/GPU), permite entrenamiento muy rápido incluso con millones de filas.
Validación cruzada	✅ Recomendable usar k-fold o repeated CV para ajustar hiperparámetros	Validación cruzada anidada o simple ayuda a elegir hiperparámetros como `eta` (learning_rate), `nrounds` (número de árboles), `max_depth`, `subsample`, `colsample_bytree`.
No funciona bien si...	❌ No es ideal con datos muy pequeños, ruido alto o target extremadamente desbalanceado sin ajuste	No conviene con datasets muy pequeños, ya que puede sobreajustar; tampoco si el ruido es muy alto y no se regula bien la complejidad.
Fuente: Elaboración propia

Gradient Boosting Machines (GBM)

Gradient Boosting Machines (GBM) es un algoritmo de aprendizaje conjunto (ensemble learning) extremadamente potente y versátil, utilizado para clasificación, regresión y otras tareas predictivas. A diferencia de Random Forest que construye árboles de forma independiente en paralelo (bagging), GBM construye los árboles de forma secuencial y aditiva. La idea central es que cada nuevo árbol en el conjunto intenta corregir los errores residuales (residuos) del conjunto de árboles construidos previamente.

El concepto fundamental detrás de GBM es el impulso (boosting), donde los modelos “débiles” (generalmente árboles de decisión, a menudo árboles poco profundos o “stumps”) se combinan para formar un modelo “fuerte”. GBM logra esto de una manera específica:

1. Modelo Inicial: Comienza con una predicción inicial para todos los datos (por ejemplo, el valor promedio para regresión o la probabilidad logarítmica para clasificación).
2. Cálculo de Residuos (Pseudo-residuos): En cada iteración, el algoritmo calcula los residuos (o más precisamente, los “pseudo-residuos” o gradientes negativos de la función de pérdida) entre los valores reales y las predicciones actuales del modelo. Estos residuos representan los “errores” que el modelo actual no ha podido capturar.
3. Entrenamiento de un Nuevo Árbol: Se entrena un nuevo árbol de decisión para predecir estos residuos. Este árbol es típicamente pequeño y débil, diseñado para centrarse en las áreas donde el modelo actual tiene los mayores errores.
4. Actualización del Modelo: La predicción de este nuevo árbol se añade a la predicción acumulada del modelo existente, multiplicada por una tasa de aprendizaje (learning rate). Esta tasa de aprendizaje controla el tamaño del paso de cada árbol, evitando que el modelo se sobreajuste rápidamente.
5. Iteración: Este proceso se repite para un número predefinido de iteraciones, o hasta que una métrica de rendimiento deje de mejorar. Cada nuevo árbol contribuye a reducir los errores restantes.

En el contexto del aprendizaje global vs. local, GBM es un sistema de aprendizaje global que se construye de manera iterativa a partir de componentes de aprendizaje local. Cada árbol individual en el proceso de boosting es un sistema de aprendizaje local (como los decision stumps o árboles poco profundos) que se enfoca en una parte específica del error. Sin embargo, la combinación aditiva y secuencial de estos modelos “débiles” produce un modelo predictivo global altamente sofisticado y preciso. Si los datos no se distribuyen linealmente, GBM aplica el concepto de regresión (o clasificación) mediante una forma incremental y adaptativa de regresión ponderada localmente. Al centrarse en los errores residuales, GBM aborda directamente la desventaja de que “a veces ningún valor de parámetro puede proporcionar una aproximación suficientemente buena” en un solo modelo. Su capacidad para minimizar la función de pérdida de forma gradual y dirigida lo hace excepcionalmente eficaz para modelar relaciones complejas y no lineales, a menudo logrando un rendimiento superior en muchos problemas del mundo real.

Guía rápida para elegir GBM
Gradient Boosting Machines (GBM)
Criterio	Aplica	Detalles
Tipo de modelo	✅ Supervisado	Ensamble de árboles secuenciales donde cada árbol corrige errores del anterior.
Variable respuesta	✅ Categórica o Continua	En clasificación se combinan probabilidades; en regresión se promedian predicciones.
Variables predictoras	✅ Numéricas y categóricas (requiere codificación)	Funciona con muchas variables y aprende la importancia automáticamente.
Relación entre variables	✅ Captura no linealidades e interacciones complejas vía boosting	Construye árboles débiles que se enfocan en los errores residuales previos.
Normalidad de residuos	❌ No requiere	No impone supuestos en la distribución de los errores.
Independencia de errores	✅ Deseable pero no obligatorio	Los datos deben ser observaciones independientes; sensible a dependencias temporales.
Homoscedasticidad	❌ No se asume homoscedasticidad	No requiere varianza constante puesto que se basa en árboles.
Sensible a outliers	⚠️ Moderadamente (los outliers pueden influir en árboles individuales)	Los outliers pueden exagerar los gradientes y forzar ajustes extremos en árboles individuales.
Multicolinealidad entre predictores	✅ Robusto (los arboles manejan colinealidad localmente)	Los árboles reducen impacto de colinealidad, pero múltiples árboles pueden still complicarla.
Interpretabilidad	⚠️ Baja (modelo de tipo caja negra con varios árboles secuenciales)	Difícil de interpretar el conjunto; se pueden usar importance plots o SHAP para explicación.
Velocidad y eficiencia	⚠️ Lento con muchos árboles, datos grandes o parámetros altos	La construcción secuencial de cientos de árboles puede ser costosa en tiempo y memoria.
Validación cruzada	✅ Recomendable con k-fold o repeated CV para ajuste de hiperparámetros	La validación cruzada ayuda a determinar tasa de aprendizaje, número de árboles y profundidad.
No funciona bien si...	❌ Si se tienen pocos datos, muchas categorías o ruido alto	No es ideal cuando se tienen muy pocos datos o categorías con pocos ejemplos.
Fuente: Elaboración propia

Gradient Boosted Regression Trees (GBRT)

Gradient Boosted Regression Trees (GBRT), a menudo conocida como Gradient Boosting Machines (GBM) cuando los modelos base son árboles de decisión de regresión, es una técnica de aprendizaje conjunto (ensemble learning) extremadamente potente y ampliamente utilizada para tareas de regresión (predicción de valores numéricos continuos) y también puede adaptarse para clasificación. Su fortaleza radica en su capacidad para construir un modelo predictivo robusto y preciso mediante la combinación secuencial de múltiples árboles de decisión “débiles”.

La idea central de GBRT se basa en el principio de boosting, donde cada nuevo árbol en el conjunto se entrena para corregir los errores residuales (la diferencia entre los valores reales y las predicciones acumuladas del modelo hasta ese momento) de los árboles construidos en las iteraciones anteriores. Este proceso es iterativo y aditivo:

1. Modelo Inicial: El proceso comienza con una predicción inicial simple para todos los datos, a menudo el valor promedio de la variable objetivo.
2. Cálculo de Pseudo-Residuos: En cada iteración, GBRT calcula los “pseudo-residuos”, que son los gradientes negativos de la función de pérdida con respecto a la predicción actual. Para la pérdida cuadrática media (común en regresión), estos pseudo-residuos son simplemente los errores tradicionales (valor real - predicción).
3. Entrenamiento de un Árbol de Regresión: Se entrena un nuevo árbol de decisión de regresión (que es un “aprendiz débil”, a menudo un árbol poco profundo o un decision stump) para predecir estos pseudo-residuos. El árbol busca los mejores puntos de división para reducir estos errores.
4. Actualización del Modelo: La predicción de este nuevo árbol de regresión se añade a la predicción acumulada del modelo existente, pero se escala por una tasa de aprendizaje (learning rate). Esta tasa de aprendizaje es un hiperparámetro crucial que controla la “contribución” de cada nuevo árbol y ayuda a prevenir el sobreajuste.
5. Iteración: Los pasos 2 a 4 se repiten para un número predefinido de iteraciones. Cada nuevo árbol se enfoca en las deficiencias del modelo combinado anterior, refinando gradualmente la predicción.

En el contexto del aprendizaje global vs. local, GBRT es un sistema de aprendizaje global que se construye de manera iterativa a partir de componentes de aprendizaje local. Cada árbol de regresión individual es un sistema de aprendizaje local que divide el espacio de características y aprende patrones en subregiones. Sin embargo, el proceso de boosting, al combinar estos árboles secuencialmente para reducir los errores residuales globales, construye una aproximación de función global altamente flexible y precisa. La clave es que, si los datos no se distribuyen linealmente, el algoritmo aplica el concepto de regresión de manera muy efectiva a través de esta regresión ponderada localmente. Al centrarse en los errores que el modelo actual no puede explicar, GBRT aborda directamente la desventaja de que “a veces ningún valor de parámetro puede proporcionar una aproximación suficientemente buena” en un solo modelo. Es excepcionalmente potente para capturar relaciones complejas y no lineales, y es ampliamente utilizado en diversas aplicaciones, desde la predicción de precios hasta la optimización de rutas.

Guía rápida para elegir GBRT
Gradient Boosted Regression Trees (GBRT)
Criterio	Aplica	Detalles
Tipo de modelo	✅ Supervisado	Ensamble de árboles de regresión secuenciales donde cada árbol corrige errores del anterior mediante gradiente.
Variable respuesta	✅ Continua (regresión)	Predice valores continuos sumando las predicciones ponderadas de múltiples árboles débiles.
Variables predictoras	✅ Numéricas y categóricas (requiere codificación para ciertas implementaciones)	Funciona con variables mixtas; las categóricas suelen transformarse en dummies.
Relación entre variables	✅ Captura no linealidades e interacciones complejas mediante boosting de árboles	Cada nuevo árbol se enfoca en los residuos del modelo anterior, capturando patrones complejos.
Normalidad de residuos	❌ No requiere supuestos de normalidad en residuos	No impone distribución normal porque optimiza una función de pérdida (por ejemplo, MSE) directamente.
Independencia de errores	✅ Deseable, aunque no obligatorio (mejor si instancias independientes)	Mejor si las observaciones no están correlacionadas en el tiempo; ajustar para series si es necesario.
Homoscedasticidad	❌ No asume homoscedasticidad	No requiere varianza constante puesto que se basa en árboles, no en un modelo paramétrico de errores.
Sensible a outliers	⚠️ Moderadamente (outliers pueden influir en árboles individuales)	Los valores extremos pueden provocar ajustes excesivos en árboles individuales; usar tasa de aprendizaje baja ayuda a mitigar.
Multicolinealidad entre predictores	✅ Robusto (los árboles reducen el impacto de colinealidad localmente)	Los árboles reducen el impacto de variables correlacionadas, aunque múltiples iteraciones pueden complicar interpretaciones.
Interpretabilidad	⚠️ Baja (modelo en su conjunto es “caja negra”)	Difícil de interpretar directamente; se puede usar importancia de variables o herramientas como SHAP para explicación.
Velocidad y eficiencia	⚠️ Lento con muchos árboles o datos extensos	Cada iteración entrena un árbol nuevo; muchos árboles o gran profundidad de árbol incrementan el tiempo de entrenamiento.
Validación cruzada	✅ Recomendable usar k-fold o repeated CV para ajuste de hiperparámetros	CV ayuda a determinar parámetros como tasa de aprendizaje (`learning_rate`), número de árboles (`n.trees`) y profundidad máxima (`max_depth`).
No funciona bien si...	❌ No es ideal si hay muy pocos datos o ruido excesivo	No es adecuado cuando el dataset es muy pequeño o extremadamente ruidoso, ya que puede sobreajustar fácilmente.
Fuente: Elaboración propia

Isolation Forest

Light Gradient Boosting Machine (LightGBM)

LightGBM (Light Gradient Boosting Machine) es otro algoritmo de Gradient Boosting Machines (GBM) de alto rendimiento, desarrollado por Microsoft. Está diseñado para ser extremadamente rápido y eficiente en el uso de memoria, especialmente con grandes conjuntos de datos, sin sacrificar una precisión significativa. Al igual que XGBoost, ha ganado popularidad en competiciones de machine learning por su velocidad y capacidad para manejar grandes volúmenes de datos.

La idea fundamental de LightGBM es la misma que la de otros algoritmos de boosting: construir un modelo aditivo de forma secuencial, donde cada nuevo árbol intenta corregir los errores residuales del modelo combinado anterior. Sin embargo, LightGBM introduce varias optimizaciones clave para lograr su notable eficiencia:

1. Gradient-based One-Side Sampling (GOSS): A diferencia de XGBoost que usa todas las instancias para cada iteración, GOSS se enfoca en las instancias que tienen un mayor gradiente (es decir, las que contribuyen más al error). Descarta las instancias con gradientes pequeños o las muestrea con menos frecuencia, lo que acelera el entrenamiento sin perder demasiada precisión.
2. Exclusive Feature Bundling (EFB): EFB agrupa características mutuamente exclusivas (es decir, características que rara vez toman valores distintos de cero al mismo tiempo) en un solo “bundle”. Esto reduce el número de características y acelera el cálculo del histograma sin afectar la precisión.
3. Histogram-based Algorithm: En lugar de construir árboles en una forma de pre-orden que es común en muchos algoritmos (lo que puede ser lento al enumerar todos los puntos de división), LightGBM utiliza un algoritmo basado en histogramas. Convierte los valores de las características continuas en bins discretos. Esto acelera significativamente el proceso de búsqueda del mejor punto de división.
4. Leaf-wise (Best-first) Tree Growth: A diferencia de la mayoría de los árboles de decisión que crecen nivel por nivel (como en XGBoost), LightGBM crece el árbol “hoja por hoja” (leaf-wise). Esto significa que en cada paso, selecciona la hoja con la mayor reducción de pérdida y la divide. Este enfoque puede llevar a árboles más profundos y asimétricos que pueden ser más precisos para el mismo número de nodos, aunque puede ser más propenso al sobreajuste (lo cual se mitiga con la regularización).

En el contexto del aprendizaje global vs. local, LightGBM, al igual que otros algoritmos de boosting, es una estrategia de aprendizaje global que se construye de manera iterativa a partir de componentes de aprendizaje local. Cada árbol que se entrena es un “aprendiz débil” que se enfoca en las deficiencias residuales del modelo acumulado. Si los datos no se distribuyen linealmente, el algoritmo aplica el concepto de regresión (o clasificación) de manera muy eficiente mediante esta regresión ponderada localmente. Al centrarse en los errores y optimizar los cálculos, LightGBM aborda de manera sobresaliente la desventaja de que “a veces ningún valor de parámetro puede proporcionar una aproximación suficientemente buena” en un solo modelo. Su énfasis en la velocidad y la eficiencia lo hace ideal para conjuntos de datos muy grandes o escenarios donde el tiempo de entrenamiento es una preocupación crítica.

Guía rápida para elegir LightGBM
LightGBM
Criterio	Aplica	Detalles
Tipo de modelo	✅ Supervisado	Ensamble supervisado que entrenan árboles de decisión usando histogram-based gradient boosting.
Variable respuesta	✅ Continua (regresión) o Categórica (clasificación)	En regresión predice valores continuos; en clasificación maximiza log-loss u otras funciones objetivo.
Variables predictoras	✅ Numéricas y categóricas (requiere codificación apropiada)	Acepta variables mixtas; las categóricas deben convertirse a formato numérico o usar encoding interno.
Relación entre variables	✅ Captura no linealidades e interacciones mediante árboles en boosting	Cada iteración ajusta un árbol enfocándose en los residuos del anterior, capturando patrones complejos.
Normalidad de residuos	❌ No requiere supuestos de normalidad	No impone distribución paramétrica de errores; optimiza la función de pérdida directamente.
Independencia de errores	✅ Deseable, aunque no obligatorio (mejor si instancias independientes)	Funciona mejor si las muestras son independientes; sensible a series de tiempo sin preparación adecuada.
Homoscedasticidad	❌ No asume homoscedasticidad	No requiere varianza constante, dado que es un método basado en árbol, no en supuestos de error.
Sensible a outliers	⚠️ Moderadamente (los outliers pueden influir en pesos de hojas)	Los valores extremos pueden afectar el cálculo de gradientes y splits; usar regularización y parámetros de manejo de outliers.
Multicolinealidad entre predictores	✅ Robusto (usa histogram-based split que atenúa colinealidad)	La división basada en histogramas reduce el impacto de predictores altamente correlacionados.
Interpretabilidad	⚠️ Baja (modelo complejo tipo ‘caja negra’)	Difícil interpretar cada árbol; se utilizan métricas de importancia y herramientas como SHAP para explicación.
Velocidad y eficiencia	✅ Muy rápido y escalable (optimized gradient-based)	Implementación en C++ altamente optimizada que permite entrenamiento muy rápido incluso con grandes volúmenes de datos.
Validación cruzada	✅ Recomendable usar k-fold o repeated CV para ajustar hiperparámetros	CV ayuda a elegir parámetros como `learning_rate`, `num_leaves`, `max_depth`, `feature_fraction`, `bagging_fraction`.
No funciona bien si...	❌ No conviene con datos muy pequeños o muy ruidosos sin regularización	No es ideal si el dataset es muy pequeño, pues el boosting puede sobreajustar; tampoco con mucho ruido sin regularización adecuada.
Fuente: Elaboración propia

Random Forest

Random Forest es un algoritmo de aprendizaje conjunto (ensemble learning) altamente popular y potente, utilizado tanto para tareas de clasificación como de regresión. Fue desarrollado por Leo Breiman en 2001 y se basa en la idea de combinar las predicciones de múltiples árboles de decisión para lograr una mayor precisión y robustez que un solo árbol. La fuerza de Random Forest reside en dos conceptos clave: bagging (bootstrap aggregation) y la aleatoriedad en la selección de características.

La idea fundamental detrás de Random Forest es construir un “bosque” de árboles de decisión de una manera específica:

1. Bagging (Bootstrap Aggregation): En lugar de entrenar un solo árbol en todo el conjunto de datos, Random Forest entrena cada árbol en una muestra de arranque (bootstrap sample) diferente. Una muestra de arranque es un subconjunto del conjunto de datos original, muestreado con reemplazo. Esto significa que algunos puntos de datos pueden aparecer varias veces en una muestra, mientras que otros pueden no aparecer en absoluto. Este muestreo genera diversidad entre los árboles.

2. Aleatoriedad en la Selección de Características: Cuando cada árbol se construye, en cada paso de división (nodo), Random Forest no considera todas las características disponibles. En cambio, solo considera un subconjunto aleatorio de características para encontrar la mejor división. Esta aleatoriedad adicional (además del muestreo de arranque) descorrelaciona aún más los árboles, lo que es crucial para el rendimiento del algoritmo. Si los árboles estuvieran altamente correlacionados, el error de un árbol promedio no se reduciría al promediar.

Una vez que se han construido numerosos árboles (típicamente cientos o miles), las predicciones se combinan: para clasificación, se utiliza la votación por mayoría (la clase más votada por los árboles individuales); para regresión, se calcula el promedio de las predicciones de todos los árboles.

En el contexto del aprendizaje global vs. local, Random Forest se puede considerar como un sistema de aprendizaje global que se construye a partir de componentes de aprendizaje local. Cada árbol individual en el bosque es un sistema de aprendizaje local (como CART, que divide el problema en subproblemas más pequeños). Sin embargo, al combinar las predicciones de muchos de estos árboles, Random Forest logra una aproximación de función global muy robusta y flexible. La ventaja es que, si los datos no se distribuyen linealmente, el algoritmo aplica el concepto de regresión (o clasificación) mediante una forma sofisticada de regresión ponderada localmente. La combinación de árboles diversos y descorrelacionados mitiga la desventaja de que “a veces ningún valor de parámetro puede proporcionar una aproximación suficientemente buena” en un solo modelo. Random Forest sobresale en capturar relaciones complejas y no lineales, manejar grandes conjuntos de datos con muchas características y es menos propenso al sobreajuste que un solo árbol de decisión grande.

Guía rápida para elegir random forest
Random Forest
Criterio	Aplica	Detalles
Tipo de modelo	✅ Supervisado	Ensamble de árboles de decisión, cada uno entrenado en una muestra bootstrap y usando un subconjunto aleatorio de predictores.
Variable respuesta	✅ Categórica o Continua	En clasificación predice la clase mayoritaria entre árboles; en regresión, el promedio de predicciones.
Variables predictoras	✅ Numéricas y categóricas (requiere codificación)	Acepta muchas variables y selecciona automáticamente las más relevantes por importancia.
Relación entre variables	✅ Captura relaciones no lineales e interacciones complejas	Al generar múltiples árboles, capta interacciones no lineales sin necesidad de especificarlas.
Normalidad de residuos	❌ No requiere	No hay supuestos sobre la distribución de los errores.
Independencia de errores	✅ Deseable pero no obligatorio	Los árboles individuales pueden manejar correlación leve; el ensamble mitiga la dependencia.
Homoscedasticidad	❌ No se asume homoscedasticidad	No necesita homogeneidad de varianza en los errores residuales.
Sensible a outliers	✅ Robusto a outliers (por agregación)	Cada árbol es poco sensible a outliers, y la agregación mejora robustez.
Multicolinealidad entre predictores	✅ Robusto (selecciona subconjuntos aleatorios)	Reduce el problema de colinealidad al seleccionar subconjuntos de variables por árbol.
Interpretabilidad	⚠️ Moderada (difícil interpretar cientos de árboles)	Es difícil de explicar, aunque se pueden usar métricas de importancia de variables.
Velocidad y eficiencia	⚠️ Lento con muchos árboles o datos grandes	Puede volverse lento si se entrenan miles de árboles en datasets muy grandes.
Validación cruzada	✅ Recomendado usar k-fold	Cross-validation ayuda a evitar overfitting y evaluar generalización.
No funciona bien si...	❌ Puede sobreajustar si no se ajustan hiperparámetros (e.g. profundidad, número de árboles)	No es ideal si el interpretabilidad es crítica o el tiempo computacional es limitado.
Fuente: Elaboración propia

Stacked Generlization (Blending)

Stacked Generalization, comúnmente conocido como Stacking, y su variante Blending, son técnicas avanzadas de aprendizaje conjunto (ensemble learning) que buscan combinar las predicciones de múltiples modelos de aprendizaje automático para obtener un rendimiento predictivo superior al de cualquier modelo individual. La idea fundamental es que, en lugar de simplemente promediar o votar las predicciones, se entrena un modelo de segundo nivel (meta-modelo) para aprender a combinar óptimamente las predicciones de los modelos de primer nivel (modelos base).

El proceso de Stacking generalmente implica dos o más “capas” de modelos:

1. Modelos Base (Nivel 0): En la primera capa, se entrenan múltiples modelos de aprendizaje automático diversos (pueden ser de diferentes tipos, como árboles de decisión, máquinas de vectores de soporte, redes neuronales, etc.). Estos modelos base se entrenan sobre el conjunto de datos de entrenamiento original (o en particiones del mismo).

2. Generación de Meta-Características: Las predicciones generadas por estos modelos base sobre un conjunto de datos “fuera de muestra” (que no se usó para entrenar los modelos base, típicamente a través de validación cruzada k-fold) se utilizan como nuevas características o “meta-características”. Estas meta-características, junto con la variable objetivo original, forman un nuevo conjunto de datos de entrenamiento para el meta-modelo.

3. Meta-Modelo (Nivel 1): En la segunda capa, se entrena un meta-modelo (a menudo un modelo más simple, como regresión lineal, regresión logística o un árbol de decisión poco profundo) utilizando estas meta-características como entrada y la variable objetivo original como salida. El meta-modelo aprende la relación entre las predicciones de los modelos base y la respuesta verdadera, y por lo tanto, cómo “pesar” o “combinar” esas predicciones de la mejor manera.

Blending es una variación más sencilla de Stacking. La principal diferencia es cómo se generan las meta-características para el meta-modelo. En Blending, se reserva una subdivisión de validación (holdout set) del conjunto de entrenamiento original. Los modelos base se entrenan en la parte restante del conjunto de entrenamiento, y luego sus predicciones sobre este conjunto de validación se utilizan directamente como meta-características para entrenar el meta-modelo. Esto simplifica el proceso de validación cruzada, pero el meta-modelo se entrena con menos datos.

En el contexto del aprendizaje global vs. local, Stacking/Blending es una estrategia de aprendizaje global que explota el poder de múltiples aproximaciones de función local (los modelos base) para construir un modelo final altamente sofisticado. Cada modelo base, dependiendo de su naturaleza, puede ser un sistema de aprendizaje local que descubre patrones en subregiones de datos. Sin embargo, el meta-modelo aprende una función de combinación global sobre las predicciones de estos modelos base. Si los datos no se distribuyen linealmente, Stacking/Blending aplica el concepto de regresión (o clasificación) de una manera muy flexible. Al permitir que un modelo de segundo nivel aprenda a combinar las predicciones de diversos modelos, supera la limitación de que “a veces ningún valor de parámetro puede proporcionar una aproximación suficientemente buena” en un solo modelo. Es particularmente eficaz en competiciones de machine learning donde se busca el máximo rendimiento, ya que aprovecha las fortalezas complementarias de diferentes algoritmos. Sin embargo, puede ser computacionalmente intensivo y más difícil de interpretar que los modelos individuales.

Guía rápida para elegir blending
Stacked Generlizaation (Blending)
Criterio	Aplica	Detalles
Tipo de modelo	✅ Supervisado	Ensamble supervisado que combina varias predicciones (base learners) mediante un modelo meta.
Variable respuesta	✅ Categórica o Continua (depende de los modelos base)	El meta-modelo acepta la salida de modelos base; puede predecir clases o valores continuos.
Variables predictoras	✅ Numéricas y/o categóricas (codificación según modelos base)	Usa predictores originales para los base learners; algunos requieren dummies, otros no.
Relación entre variables	✅ Captura relaciones complejas vía combinación de modelos base	Aprende patrones no lineales e interacciones complejas a través de múltiples capas.
Normalidad de residuos	❌ No exige supuestos de normalidad en residuos	No impone distribución normal: cada base learner tiene sus propios supuestos.
Independencia de errores	✅ Deseable, pero no obligatorio (mejor si observaciones independientes)	Ideal si cada muestra es independiente; sensibles a dependencias en validaciones cruzadas.
Homoscedasticidad	❌ No se asume homoscedasticidad	No requiere varianza constante, ya que se basa en agregación de predicciones.
Sensible a outliers	⚠️ Moderadamente (outliers afectan modelos base individuales)	Modelos base (p. ej. ARBOTS, SVM) pueden verse influenciados por valores extremos;
Multicolinealidad entre predictores	⚠️ Puede verse afectado (depende de base learners y correlated features)	Modelos base diversificados reducen colinealidad, pero meta-modelo puede verse afectado.
Interpretabilidad	⚠️ Baja (modelo meta difícil de interpretar directamente)	Difícil atribuir importancia directa; se pueden usar técnicas como SHAP para interpretación.
Velocidad y eficiencia	⚠️ Lento en entrenamiento y predicción, según número de base learners	Entrenamiento de múltiples base learners y meta-modelo incrementa tiempo; predicción también más lenta.
Validación cruzada	✅ Esencial (usar CV anidada para entrenar meta-modelo)	Usar validación cruzada anidada: inner folds para entrenar base learners y stacking, outer folds para evaluar.
No funciona bien si...	❌ Si datos muy escasos o muy ruidosos, riesgo de sobreajuste	No recomendable si hay muy pocos datos (stacking requiere dividir en folds) o si los base learners no aportan diversidad.
Fuente: Elaboración propia