🔍 1. Regresión
Ejemplos: Regresión Lineal Simple, Regresión Ridge, Regresión Lasso.
Uso: Ideal para predecir valores numéricos continuos (como precios o temperaturas) y cuando esperas relaciones lineales entre tus variables.
Ventajas: Es un modelo simple de entender y altamente interpretable.
Limitaciones: Su desempeño es bajo cuando las relaciones entre las variables son no lineales o muy complejas.
Ordinary Least Squares Regression (OLSR)
Ordinary Least Squares Regression (OLSR) en R
Ordinary Least Squares Regression (OLSR) en Python
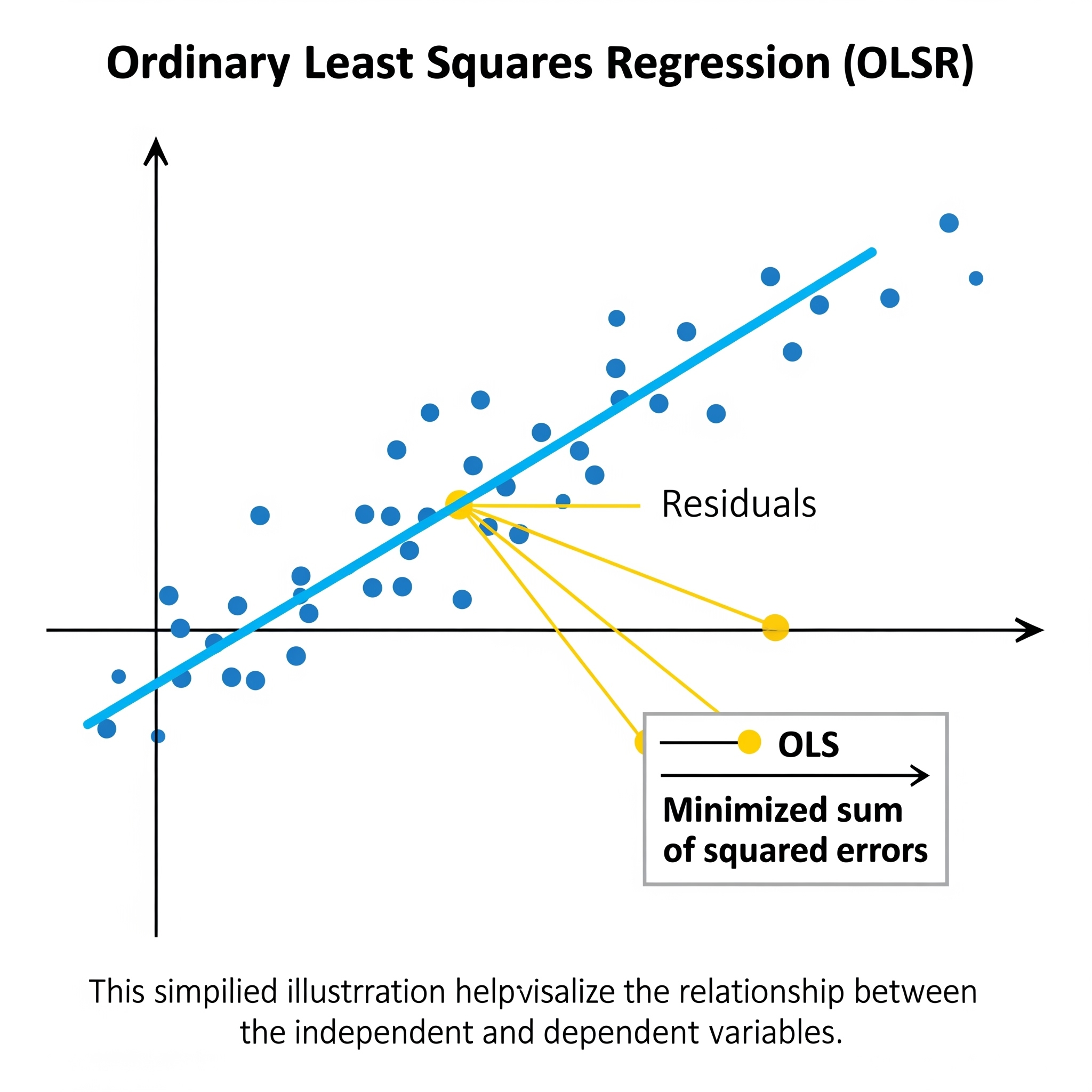
La Regresión por Mínimos Cuadrados Ordinarios (OLS) es una técnica fundamental en estadística y Machine Learning para modelar la relación lineal entre una variable dependiente (a predecir) y una o más variables independientes. Su objetivo es encontrar la línea (o hiperplano) que mejor se ajusta a los datos, minimizando la suma de los cuadrados de las diferencias entre los valores reales y los predichos por el modelo. Es decir, busca los coeficientes que hacen que la distancia (al cuadrado) de los puntos a la línea sea mínima.
Los coeficientes de OLS se pueden calcular directamente con una fórmula matemática, sin necesidad de procesos iterativos complejos, bajo ciertos supuestos como la linealidad de la relación y la independencia de los errores.
En el contexto del aprendizaje global vs. local, OLS es un ejemplo claro de un modelo de aprendizaje global. OLS busca una única ecuación o un conjunto de coeficientes que describan la relación entre las variables para todo el conjunto de datos. La línea o hiperplano que encuentra es una solución global que se aplica de manera uniforme en todo el espacio de características. Esto la hace muy interpretable y computacionalmente eficiente, pero limitada si la relación real entre las variables no es estrictamente lineal en todo el dominio de los datos.
Linear Regression
La Regresión Lineal es uno de los algoritmos más fundamentales y ampliamente utilizados en el campo del Machine Learning y la estadística. Es un modelo supervisado que busca establecer una relación lineal entre una variable de respuesta (o dependiente) continua y una o más variables predictoras (o independientes).
Concepto y Ecuación:
La idea central de la regresión lineal es encontrar la línea (o hiperplano en múltiples dimensiones) que mejor se ajusta a los datos, de modo que se pueda predecir el valor de la variable dependiente basándose en los valores de las variables predictoras.
- Regresión Lineal Simple: Implica una única variable predictora. La ecuación de la línea es: \[Y = \beta_0 + \beta_1 X + \epsilon\]
Donde: * \(Y\) es la variable de respuesta. * \(X\) es la variable predictora. * \(\beta_0\) es el intercepto (el valor de \(Y\) cuando \(X\) es 0). * \(\beta_1\) es el coeficiente de la pendiente (cuánto cambia \(Y\) por cada unidad de cambio en \(X\)). * \(\epsilon\) es el término de error o residual (la parte de \(Y\) que el modelo no puede explicar).
-
Regresión Lineal Múltiple: Implica dos o más variables predictoras. La ecuación se extiende a:
\[Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + ... + \beta_p X_p + \epsilon\]
Donde: * \(X_1, X_2, ..., X_p\) son las \(p\) variables predictoras. * \(\beta_1, \beta_2, ..., \beta_p\) son los coeficientes de cada variable predictora.
Cómo Funciona (Mínimos Cuadrados Ordinarios - OLS):
El método más común para estimar los coeficientes (\(\beta\)s) en la regresión lineal es el de Mínimos Cuadrados Ordinarios (OLS). OLS funciona minimizando la suma de los cuadrados de los residuos. Un residuo es la diferencia entre el valor real de \(Y\) y el valor predicho por el modelo (\(\hat{Y}\)).
\[\text{Minimizar: } \sum_{i=1}^{n} (Y_i - \hat{Y}_i)^2 = \sum_{i=1}^{n} (Y_i - (\beta_0 + \beta_1 X_{i1} + ... + \beta_p X_{ip}))^2\]
Al minimizar esta suma de cuadrados, OLS encuentra los coeficientes que hacen que la línea de regresión esté lo más cerca posible de la mayoría de los puntos de datos.
Supuestos Clave:
La validez de los resultados de la regresión lineal tradicional se basa en varios supuestos:
- Linealidad: La relación entre las variables \(X\) y \(Y\) es lineal.
- Independencia: Las observaciones son independientes entre sí.
- Normalidad de los Residuos: Los residuos se distribuyen normalmente.
- Homocedasticidad: La varianza de los residuos es constante a lo largo de todos los niveles de las variables predictoras.
- No Multicolinealidad Perfecta: Las variables predictoras no deben estar perfectamente correlacionadas entre sí.
Uso y Limitaciones:
La regresión lineal es popular por su simplicidad, interpretabilidad y por ser un buen punto de partida para muchos problemas de predicción. Sin embargo, su principal limitación es que solo puede modelar relaciones lineales. Si la relación subyacente entre las variables es no lineal, una regresión lineal puede no capturarla adecuadamente y dar resultados inexactos.
Aprendizaje Global vs. Local:
La Regresión Lineal es un modelo de aprendizaje puramente global.
Aspecto Global: La Regresión Lineal aprende un único conjunto de coeficientes que define una línea (o hiperplano) global que se aplica a todo el espacio de características. Esta línea busca representar la relación lineal promedio o general entre las variables predictoras y la variable de respuesta a lo largo de todo el rango de los datos. La predicción para cualquier nueva instancia se realiza utilizando la misma ecuación lineal, sin importar en qué parte del espacio de características se encuentre. No hay adaptaciones o modelos separados para diferentes subregiones de los datos; el modelo es una función que describe una tendencia general y global.
Rigidez de la Linealidad: Debido a su naturaleza global y lineal, la regresión lineal no puede capturar relaciones no lineales o interacciones complejas entre las variables predictoras de forma inherente. Si la relación real en los datos es no lineal, el modelo lineal intentará ajustarla con la mejor línea recta posible, lo que podría llevar a un bajo rendimiento.
Regresión Logística (Logit)
Figure 1: Elaboración propia
La Regresión Logística es un modelo estadístico usado principalmente para problemas de clasificación binaria, donde el objetivo es predecir la probabilidad de que una instancia pertenezca a una de dos clases (por ejemplo, “sí” o “no”, “0” o “1”). A pesar de su nombre, no predice un valor continuo, sino una probabilidad.
Este modelo utiliza una función sigmoide (o logística) para transformar una combinación lineal de las variables de entrada en un valor entre 0 y 1, que se interpreta como una probabilidad. Los coeficientes del modelo se aprenden maximizando la verosimilitud de observar los datos, generalmente a través de algoritmos como el descenso de gradiente.
En el contexto del aprendizaje global vs. local, la Regresión Logística es un modelo de aprendizaje global. Esto significa que busca un único conjunto de coeficientes que definen una frontera de decisión (un hiperplano) que se aplica a todo el espacio de características para separar las clases. Asume una relación lineal entre las variables de entrada y el logaritmo de la probabilidad, y una vez entrenado, usa esta relación global para hacer predicciones en cualquier parte del espacio de datos. Si bien es eficiente y muy interpretable, su naturaleza global puede limitar su rendimiento en casos donde las fronteras de decisión son inherentemente no lineales o muy complejas.
| Guía rápida para elegir logit | ||
| Regresión logística | ||
| Criterio | Aplica | Detalles |
|---|---|---|
| Fuente: Elaboración propia | ||
Least Angle Regression (LARS)
Least Angle Regression (LARS) es un algoritmo de regresión lineal desarrollado por Bradley Efron, Trevor Hastie, Iain Johnstone y Robert Tibshirani. Es particularmente interesante porque puede considerarse como una versión más eficiente y paso a paso de LASSO (Least Absolute Shrinkage and Selection Operator) y es útil para seleccionar características y manejar datos de alta dimensión.
A diferencia de OLS, que calcula todos los coeficientes de una vez, o de Lasso, que requiere optimización más compleja, LARS opera de manera incremental. Su idea central es avanzar los coeficientes de forma que su ángulo con el vector de residuos sea siempre el mismo y que sea el “más pequeño” posible.
El proceso de LARS se puede resumir así:
- Inicio: Todos los coeficientes se inicializan en cero.
- Identificación del Predictor más Correlacionado: El algoritmo encuentra la variable predictora que está más correlacionada con la variable de respuesta (o con el residuo actual).
- Movimiento en la Dirección del Predictor: El coeficiente de esa variable predictora se mueve gradualmente desde cero en la dirección del signo de su correlación. A medida que el coeficiente se mueve, el residuo cambia.
- Activación de Nuevos Predictores: Cuando otra variable predictora alcanza la misma correlación con el residuo actual que la variable que ya está activa, el algoritmo cambia de dirección. Ahora, los coeficientes de ambas variables activas se mueven juntas en un “ángulo equiestadístico” de tal manera que permanecen igualmente correlacionadas con el residuo.
- Proceso Iterativo: Este proceso continúa, añadiendo nuevas variables al conjunto de variables “activas” (es decir, aquellas con coeficientes distintos de cero) a medida que estas alcanzan la misma correlación con el residuo. Los coeficientes se mueven de forma coordinada.
- Criterio de Parada: El algoritmo se detiene cuando todos los predictores han sido incluidos en el modelo, o cuando se alcanza un número predefinido de pasos o de variables.
Relación con otros modelos: * Si LARS se detiene cuando los coeficientes de las variables no activas son menores o iguales a la correlación actual de las variables activas (y los coeficientes de las variables no activas se fijan en cero si su correlación es menor), entonces genera la solución completa del camino de LASSO. * También puede generar el camino de soluciones para la Ridge Regression si se modifica ligeramente.
LARS es eficiente porque solo requiere un número de pasos igual al número de variables, o menos si se detiene antes.
Aprendizaje Global vs. Local:
Least Angle Regression (LARS) es un modelo de aprendizaje global.
Aspecto Global: LARS construye un modelo lineal global paso a paso. Aunque el algoritmo añade variables una por una y ajusta sus coeficientes de manera incremental, el modelo resultante en cada paso es una ecuación de regresión lineal que se aplica a todo el conjunto de datos. La decisión de qué variable añadir y cómo ajustar los coeficientes se basa en las correlaciones globales entre las variables predictoras y la respuesta (o el residuo). La finalidad es encontrar los coeficientes óptimos para una función de regresión que se aplica a todo el espacio de características.
Selección de Características Globalmente: La capacidad de LARS para realizar selección de características (al igual que LASSO) es un proceso global. Se identifican las variables más influyentes en el contexto de todo el conjunto de datos, y su inclusión en el modelo contribuye a la formación de una relación global entre los predictores y la respuesta. No se construyen modelos separados para diferentes subregiones de los datos; en cambio, se construye un único modelo global de manera progresiva.
| Guía rápida para elegir LARS | ||
| Least Angle Regression (LARS) | ||
| Criterio | Aplica | Detalles |
|---|---|---|
| Fuente: Elaboración propia | ||
Locally Estimated Scatterplot Smoothing (LOESS)
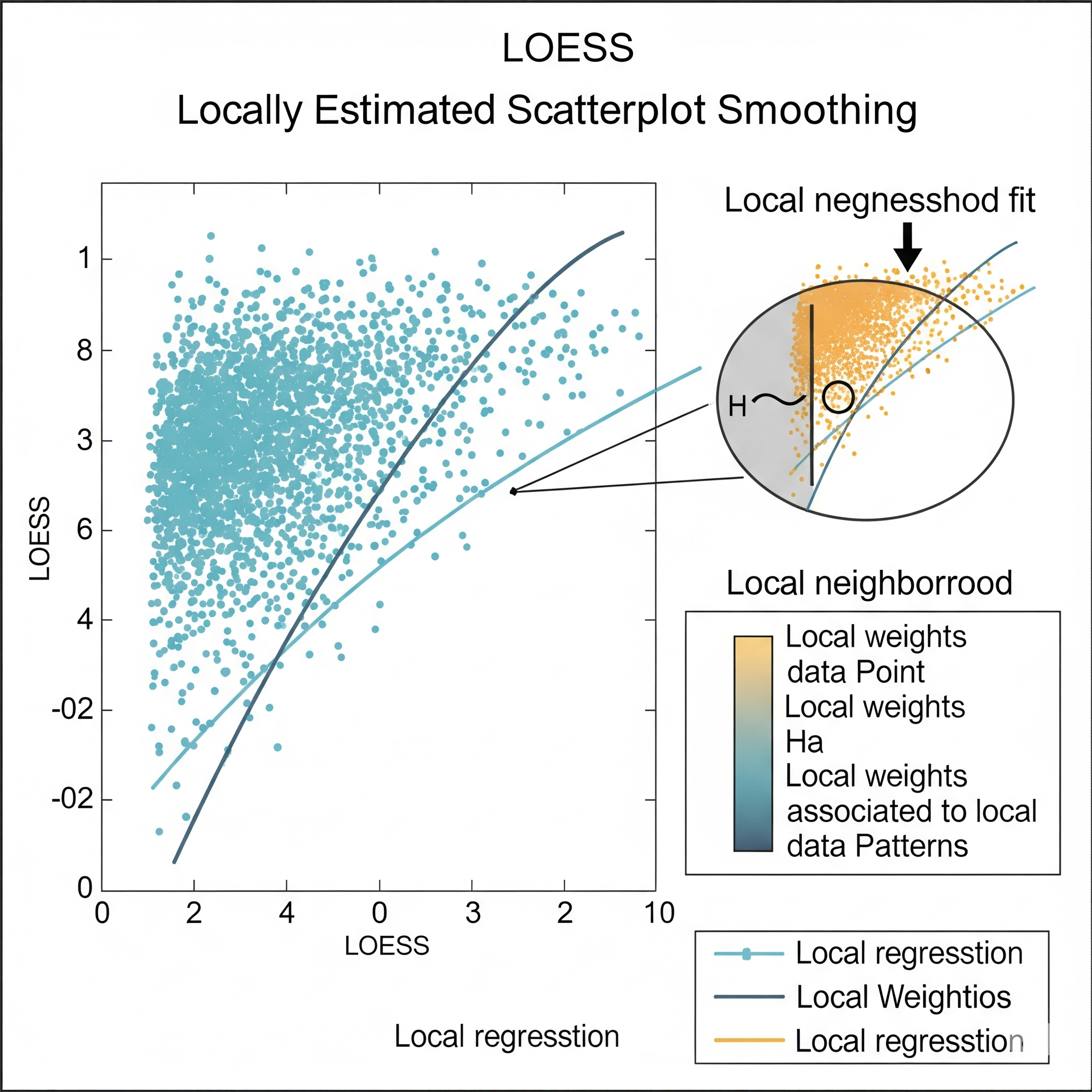
LOESS (Locally Estimated Scatterplot Smoothing), o LOWESS, es una técnica de regresión no paramétrica para crear una curva suave que se ajusta a los datos en un diagrama de dispersión. Su gran ventaja es que no asume una forma funcional global específica para la relación entre las variables, lo que la hace muy flexible para identificar tendencias y patrones no lineales.
El principio de LOESS es simple: para estimar el valor suavizado en un punto, se seleccionan los puntos de datos cercanos (definido por un parámetro de “span” o ancho de banda), se les asignan pesos (dando más peso a los puntos más cercanos), y luego se ajusta un polinomio de bajo grado (comúnmente lineal o cuadrático) a esos puntos usando mínimos cuadrados ponderados. Este proceso se repite para cada punto de interés para construir la curva.
En el contexto del aprendizaje global vs. local, LOESS es un modelo de aprendizaje puramente local. Su flexibilidad reside en que ajusta múltiples modelos simples y locales (regresiones ponderadas) en diferentes vecindarios de los datos. No busca una única ecuación global que describa la relación en todo el conjunto de datos. Esto le permite adaptarse maravillosamente a las variaciones en las relaciones y curvaturas de los datos, lo que es especialmente útil cuando los datos no se distribuyen linealmente. Sin embargo, su naturaleza local implica que no produce una fórmula explícita del modelo, y puede ser computacionalmente más intensivo para conjuntos de datos muy grandes.
| Guía rápida para elegir LOESS | ||
| Locally Estimated Scatterplot Smoothing (LOESS) | ||
| Criterio | Aplica | Detalles |
|---|---|---|
| Fuente: Elaboración propia | ||
Multivariate Adaptive Regression Splines (MARS)
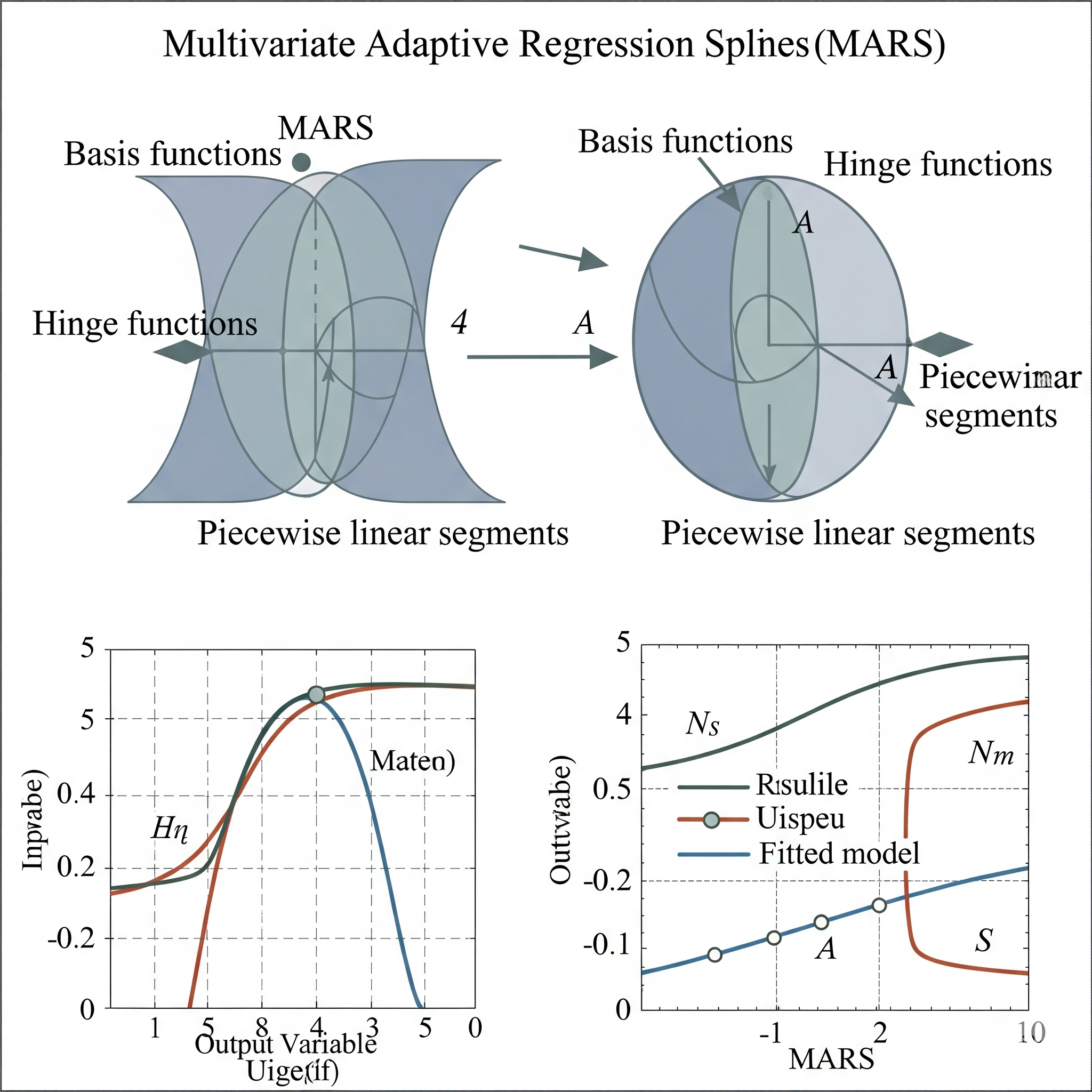
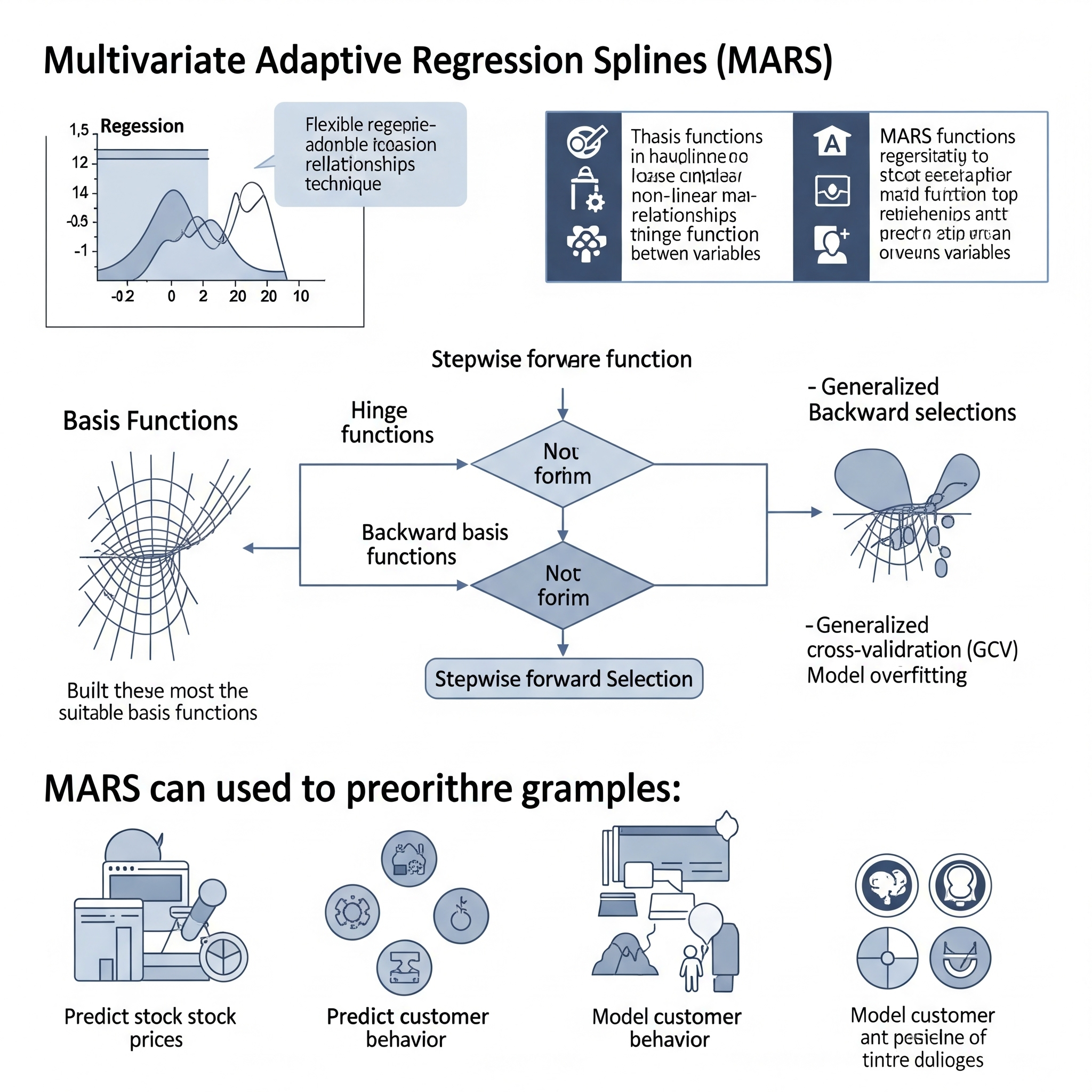
Multivariate Adaptive Regression Splines (MARS) es un algoritmo de regresión no paramétrica que extiende los modelos lineales para manejar relaciones no lineales y complejas. Desarrollado por Jerome Friedman, MARS construye su modelo al dividir el espacio de entrada en múltiples regiones y ajustar una función lineal simple (o de orden superior) a cada región.
El proceso de MARS consta de dos fases: una fase de adelante que añade iterativamente funciones base (pares de funciones “hinge” o bisagra) y nudos (puntos de corte) para capturar no linealidades e interacciones entre variables, y una fase de atrás que poda las funciones base menos significativas utilizando criterios como la Validación Cruzada Generalizada (GCV) para prevenir el sobreajuste. Esto permite a MARS ser adaptable a las particularidades de los datos.
En el contexto del aprendizaje global vs. local, MARS se sitúa como un modelo de aprendizaje adaptativo que combina aspectos globales y locales. Es “local” en el sentido de que sus funciones base y nudos dividen el espacio de datos en regiones, y dentro de cada región se aplica una relación simple. Sin embargo, es “global” porque la suma de todas estas funciones base forma una única ecuación que describe la relación en todo el conjunto de datos y se aplica de forma consistente. Esto significa que si los datos no se distribuyen linealmente, MARS puede aprender y modelar estas relaciones complejas de forma adaptativa, encontrando automáticamente dónde y cómo las relaciones cambian, ofreciendo una solución que es tanto flexible como interpretable.
| Guía rápida para elegir MARS | ||
| Splines de Regresión Adaptativa Multivariante (MARS) | ||
| Criterio | Aplica | Detalles |
|---|---|---|
| Fuente: Elaboración propia | ||
Stepwise Regression
Figure 2: Elaboración propia
La Regresión por Pasos (Stepwise Regression) es una técnica para construir un modelo de regresión lineal (o a veces otros modelos lineales generalizados) seleccionando las variables predictoras de forma iterativa y automática. Su objetivo es encontrar un subconjunto óptimo de variables que mejore la capacidad predictiva del modelo sin incluir variables irrelevantes o redundantes. Esto ayuda a simplificar el modelo, mejorar la interpretabilidad y reducir el riesgo de sobreajuste.
Existen tres estrategias principales para la regresión por pasos:
-
Selección Hacia Adelante (Forward Selection):
- Comienza con un modelo que no incluye ninguna variable predictora (solo el intercepto).
- En cada paso, evalúa todas las variables predictoras disponibles que aún no están en el modelo.
- Añade al modelo la variable que, al ser incluida, produce la mayor mejora estadística (generalmente medida por un valor p bajo, un R-cuadrado ajustado mayor, o un criterio de información como AIC o BIC).
- El proceso continúa hasta que ninguna de las variables restantes mejora el modelo por encima de un umbral predefinido.
-
Eliminación Hacia Atrás (Backward Elimination):
- Comienza con un modelo que incluye todas las variables predictoras posibles.
- En cada paso, evalúa las variables predictoras que actualmente están en el modelo.
- Elimina del modelo la variable que es menos significativa estadísticamente (generalmente medida por un valor p alto, o una reducción en el R-cuadrado ajustado o un aumento en AIC/BIC).
- El proceso continúa hasta que la eliminación de cualquier variable empeoraría significativamente el modelo.
-
Híbrida (Mixed / Bidirectional Stepwise):
- Combina la selección hacia adelante y la eliminación hacia atrás.
- En cada paso, el algoritmo puede tanto añadir una variable si mejora el modelo, como eliminar una variable que ya está en el modelo si se vuelve redundante o no significativa. Esto permite que el modelo reconsidere variables que fueron añadidas o eliminadas en pasos anteriores. Es el enfoque más común y robusto.
Criterios de Selección:
La decisión de añadir o eliminar una variable en cada paso se basa en criterios estadísticos, siendo los más comunes: * Valores p: Umbrales para la significancia estadística de los coeficientes. * \(R^2\) ajustado: Mide la proporción de varianza explicada por el modelo, penalizando la inclusión de variables innecesarias. * Criterio de Información de Akaike (AIC): Penaliza la complejidad del modelo (número de parámetros) en relación con su bondad de ajuste. * Criterio de Información Bayesiano (BIC): Similar al AIC, pero con una penalización más fuerte por la complejidad.
Ventajas y Desventajas:
- Ventajas: Puede ayudar a construir modelos más parsimoniosos, mejorar la interpretabilidad y reducir la multicolinealidad.
-
Desventajas:
- Sobreajuste: Puede llevar a sobreajuste si se usa de forma acrítica, ya que el algoritmo se optimiza para los datos de entrenamiento.
- Problemas de Significancia Estadística: Los valores p y otras métricas pueden no ser confiables debido a la selección de características basada en los datos.
- Inestabilidad: El conjunto de variables seleccionadas puede ser muy sensible a pequeñas perturbaciones en los datos o a la elección del criterio de selección.
- Ignora el Conocimiento del Dominio: Puede seleccionar variables que son estadísticamente significativas pero que carecen de sentido práctico o causal.
- No Maneja Interacciones Complejas: Es fundamentalmente un método para seleccionar variables para un modelo lineal y no está diseñado para descubrir relaciones no lineales o interacciones complejas.
Debido a sus desventajas, la regresión por pasos se utiliza con más cautela hoy en día. A menudo se prefieren métodos de regularización (como Lasso o Elastic Net) para la selección de características, ya que son más estables y realizan la selección de forma más robusta.
Aprendizaje Global vs. Local:
La Regresión por Pasos es un modelo de aprendizaje global.
Aspecto Global: La regresión por pasos construye un único modelo de regresión lineal global que busca explicar la relación entre las variables predictoras y la respuesta en todo el conjunto de datos. La selección de variables se realiza para optimizar el rendimiento de este modelo global. Los coeficientes finales que se obtienen definen una función lineal que se aplica de manera consistente a cualquier nueva observación, sin importar en qué parte del espacio de características se encuentre.
Proceso de Selección (Global): Aunque el proceso es iterativo y añade/elimina variables, la decisión en cada paso se basa en cómo esa adición/eliminación afecta la bondad de ajuste o la complejidad del modelo en todo el conjunto de datos. No se ajustan modelos separados o locales para diferentes regiones.
Support Vector Machine (SVM)
Support Vector Machine (SVM) es un potente y versátil algoritmo de Machine Learning que se utiliza tanto para tareas de clasificación como de regresión, aunque es más conocido por su aplicación en clasificación. Su objetivo principal es encontrar el hiperplano óptimo que separe las clases en el espacio de características con el margen más grande posible. Los puntos de datos más cercanos a este hiperplano se llaman vectores de soporte, y son cruciales para definir la frontera de decisión.
Para manejar datos que no son linealmente separables, SVM utiliza el “truco del kernel”. Este truco permite a SVM mapear implícitamente los datos a un espacio de mayor dimensión donde las clases podrían ser linealmente separables, sin necesidad de calcular explícitamente las coordenadas. Funciones kernel comunes como el Radial Basis Function (RBF) o Gaussiano permiten a SVM modelar fronteras de decisión no lineales complejas en el espacio original de baja dimensión.
En el contexto del aprendizaje global vs. local, SVM se clasifica principalmente como un modelo de aprendizaje global. Esto se debe a que busca un único hiperplano óptimo (o una frontera de decisión no lineal definida por el kernel) que se aplica a la totalidad del espacio de características. Una vez entrenado, el modelo predice evaluando la posición de un nuevo punto con respecto a esta frontera global. Sin embargo, hay un matiz “local” en su funcionamiento: la determinación de este hiperplano depende críticamente solo de los vectores de soporte, que son los puntos de datos “más difíciles” cercanos a la frontera. Los puntos que están lejos del margen no influyen en la definición del modelo. Aunque la frontera de decisión es una función global que se aplica en todas partes, su construcción está influenciada por estos puntos localmente relevantes, permitiendo a SVM adaptar su aproximación incluso cuando las relaciones en los datos no se distribuyen linealmente, al encontrar la separación óptima en un espacio transformado.
| Guía rápida para elegir SVM | ||
| Support Vector Machine (SVM) | ||
| Criterio | Aplica | Detalles |
|---|---|---|
| Fuente: Elaboración propia | ||